Теоретические сведения. Метод наименьших квадратов (МНК) – один из наиболее часто используемых методов при обработке эмпирических данных

Метод наименьших квадратов (МНК) – один из наиболее часто используемых методов при обработке эмпирических данных, построении и анализе физических, биологических, технических, экономических и социальных моделей[*].

С помощью МНК решают задачу выбора параметров функции (заранее заданного вида) для приближённого описания зависимости величины у от величины х.

Исходные данные могут носить самый разнообразный характер и относиться к различным отраслям науки или техники, например:

ü зависимость продолжительности службы электрических ламп 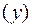от поданного на них напряжения ;

ü зависимость пробивного напряжения конденсаторов 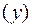от температуры окружающей среды ;

ü зависимость предела прочности стали 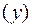от содержания углерода ;

ü зависимость показателей безработицы 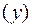и инфляции ;

ü зависимость роста преступности 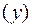,% и роста безработицы ,%

ü зависимость цен товара 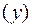от спроса на этот товар;

ü зависимость частного потребления 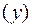от располагаемого дохода ;

ü зависимость температура воздуха 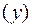от высоты над уровнем моря и другие зависимости.

Пусть необходимо установить функциональную зависимость между двумя эмпирическими данными x и y, значения которых занесены в следующую таблицу:

x	x1	x2	…	xi	…	xn
y	y1	y2	…	yi	…	yn

Точки 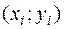координатной плоскости принято называть экспериментальными.

Установим вид функции 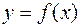по характеру расположения на координатной плоскости экспериментальных точек.

Если точки расположены так, как показано на рис.1, то разумно предположить, что между x и y существует линейная зависимость, выражающаяся формулой:

. (1)

Рассмотрим случай такой зависимости.

Уравнение (1) можно представить в виде

.

Так как точки 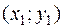, , …, 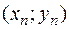не обязательно лежат на одной прямой, то, подставляя вместо х и у значения координат этих точек в выражение 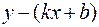, получаем равенства:

, , …, ,

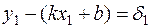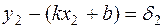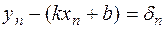где 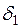, , …, 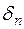– некоторые числа, которые называют погрешностями (отклонениями, невязками).

Понятно, что чем меньше эти погрешности по абсолютной величине, тем лучше прямая, задаваемая уравнением , описывает зависимость между экспериментально полученными значениями x и y.

Сущность метода наименьших квадратов заключается в подборе коэффициентов k и b таким образом, чтобы сумма квадратов погрешностей была как можно меньшей:

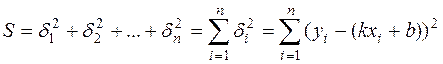
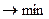(2)

Отметим, что в равенстве (2) находится сумма именно квадратов погрешностей, так как в случае суммирования самих погрешностей 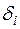сумма может оказаться малой за счет разных знаков погрешностей.

Так как в равенстве (2) x_i и y_i – заданные числа, а k и b – неизвестные, то сумму S можно рассмотреть как функцию двух переменных k и b: . Исследуем ее на экстремум:

Необходимое условие существования экстремума функции двух переменных:

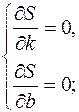
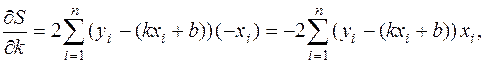
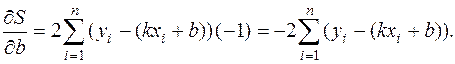
Приравнивая эти частные производные к нулю, получаем линейную систему двух уравнений с двумя переменными k и b:

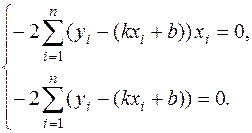
Преобразуя первое уравнение системы, получим .

Преобразуя второе уравнение системы, получим

.

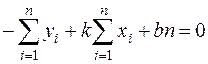Откуда имеем систему:

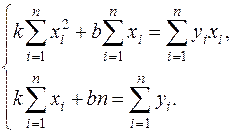(3)

Система (3) называется нормальной системой.

Из этой системы находим k и b, которые затем подставляем в уравнение (1) и получаем искомое уравнение прямой.

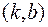Тот факт, что функция в найденной точке имеет именно минимум, устанавливается с помощью частных производных второго порядка.

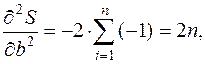
Вычислим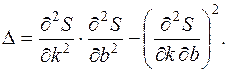

[†]

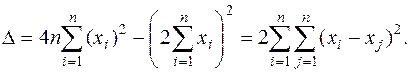Очевидно, 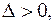следовательно, в найденной точке 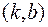функция имеет экстремум; а так как 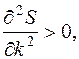то, согласно достаточному условию экстремума функции двух переменных, в точке 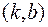функция имеет минимум.

Полученная функция называется линейной регрессией, а коэффициенты k и b – коэффициентами регрессии (величины у на х).

Зависимость между экспериментально полученными величинами может быть близка к квадратичной (рис.2). В этом случае задача состоит в нахождении коэффициентов a₂, a₁, a₀ для составления уравнения вида .

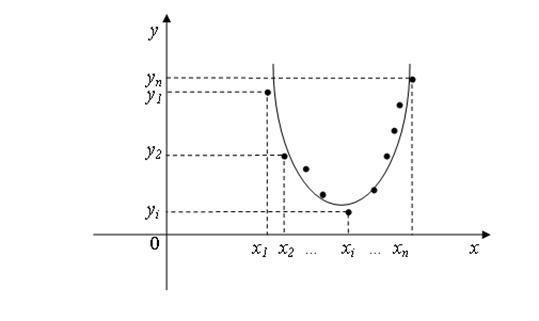
Можно доказать, что для определения коэффициентов a₂, a₁, a₀ следует решить систему уравнений:

В экспериментальной практике в качестве приближающих функций, помимо линейной и квадратичной , в зависимости от характера точечного графика часто используются следующие приближающие функции:

, , , , , .

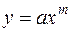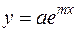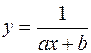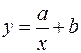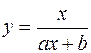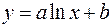Очевидно, что когда вид приближающей функции установлен, задача сводится только к отысканию значений параметров.

Пример

Д.И. Менделеев в труде «Основы химии» приводит данные растворимости у натриевой селитры 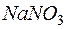на 100 г воды в зависимости от температуры t ⁰:

ti0
yi	66,7	71,0	76,3	80,6	85,7	92,9	99,4	113,6	125,1

Соответствующая зависимость может быть представлена линейной функцией .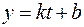

Требуется найти аппроксимирующую (приближаемую) функцию в предположении, что она является линейной.

Найдем коэффициенты k и b.

Для этого составим и решим нормальную систему уравнений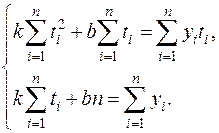

n – число эмпирических точек, n = 9.

Выполним предварительные расчеты и для удобства занесем их в таблицу (столбцы , , , )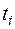

№
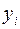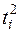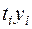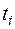
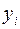
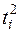
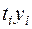
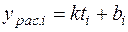
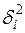
1		66,7			67,55	-0,85	0,7225
2		71,0			71,03	-0,03	0,0009
3		76,3			76,25	0,05	0,0025
4		80,6			80,6
5		85,7		1799,7	85,82	-0,12	0,0144
6		92,9		2694,1	92,78	0,12	0,0144
7		99,4				1,4	1,96
8		113,6		5793,6	111,92	1,68	2,8224
9		125,1		8506,8	126,71	-1,61	2,5921
∑		811,3		24529,2			8,19

Таким образом, нормальная система принимает вид

Решая систему, находим

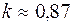
Следовательно, уравнение искомой прямой

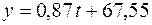
Вычислим теперь для исходных значений 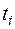расчетные значения 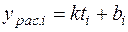и занесем полученные результаты в таблицу (столбец )

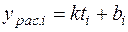Найдем 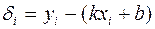и занесем результаты в таблицу (столбец ).

Вычислим сумму квадратов отклонений

.