Площадь криволинейной трапеции

Пусть функция y=f (x) определена, непрерывна и неотрицательна на отрезке 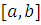тогда плоская фигура, ограниченная дугой графика функции на этом отрезке и прямыми x = a, x = b, y = 0, называется криволинейной трапецией.

Площадь криволинейной трапеции определяется по формуле:

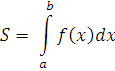
3.2 Площадь сложной фигуры

Под сложной фигурой будем понимать часть плоскости, ограниченную непрерывными на отрезке 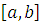кривым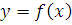и и 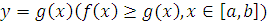и прямыми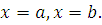

Площадь сложной фигуры находится по формуле:

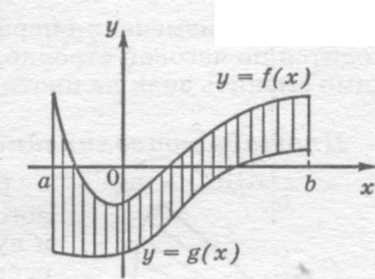
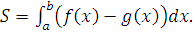
Распространенной является постановка задачи о площади плоской фигуры, ограниченной двумя кривыми. Предполагается, что эти кривые, пересекаясь, образуют некоторую ограниченную фигуру. В этом случае пределы интегрирования 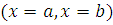заранее не известны и должны быть определены из решения системы уравнений:

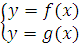
Если задача поставлена конкретно, то эта система имеет два решения, которые определяют координаты точек пересечения кривых.

Примеры:

1)Вычислить площадь фигуры, ограниченной линиями

Данная фигура сверху ограничена прямой 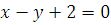снизу – параболой 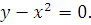(рис. 12.5). Искомую площадь вычислим по формуле. Предварительно находим пределы интегрирования и выражения для 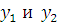. Пределами интегрирования будут абсциссы точек пересечения параболы и прямой. Решая систему уравнений

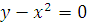
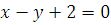
Находим 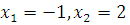, т.е. 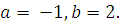Выражая 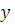из каждого уравнения, получаем

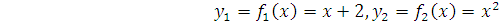
(через 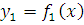обозначена функция, график которой ограничивает криволинейную фигуру сверху).

По формуле находим

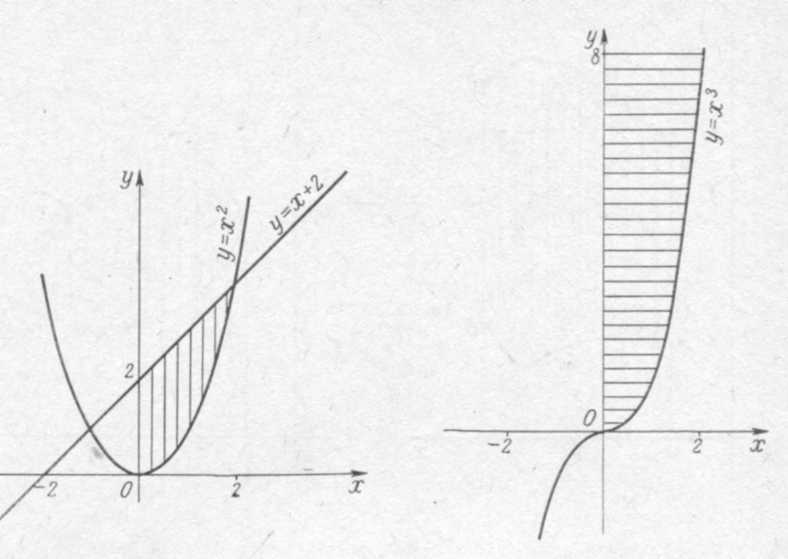
Рис. 12.5 Рис. 12.6

.

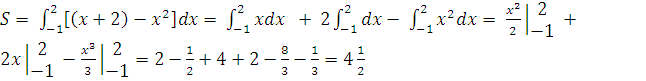2) Вычислить площадь фигуры, ограниченной осью 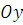и линиями 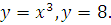(рис. 12.6)

Из уравнения 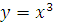находим 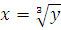и применяем формулу. Пределы интегрирования 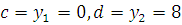найдены в результате решения системы уравнений 1) y= 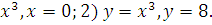По указанной формуле получаем

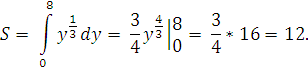
3)Вычислить площади фигур, ограниченных линиями:

а)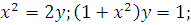

б)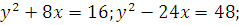

в)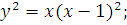

Решение:

а) Плоская фигура ограничена параболой 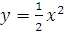и графиком функции .

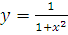Находим точки пересечения графиков:

;

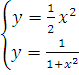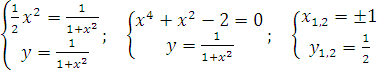
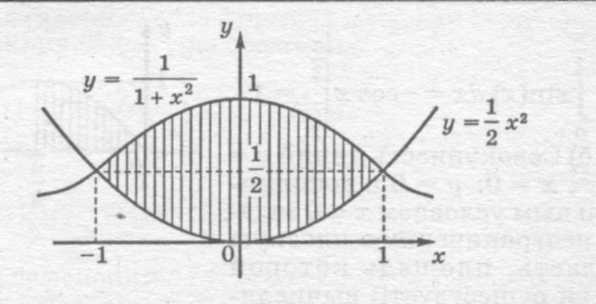
Следовательно, графики пересекаются в точках

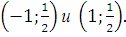
Так как исходные функции - четные, то ограничиваемая ими фигура симметрична относительно оси Оy. Воспользуемся этим обстоятельством: .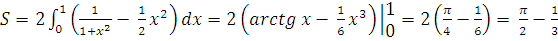

б) Уравнения 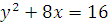и 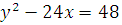задают графики парабол, осью симметрии которых является ось

Каноническое уравнение первой параболы: 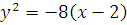, следовательно, ее вершина находится в точке 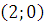; ветви направлены в отрицательном направлении оси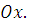

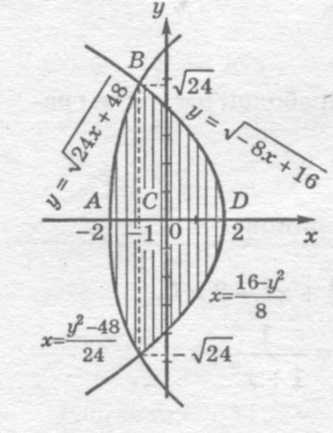
Каноническое уравнение второй параболы: 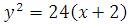; ее вершина расположена в точке 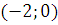; ветви направлены в положительном направлении оси

Находим точки пересечения парабол:

Параболы пересекаются в точках 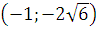и .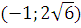

Очевидно, что искомая фигура симметрична относительно оси 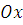, поэтому достаточно найти площадь верхней части фигуры криволинейного треугольника .

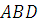Возможны два варианта расчета площади S:

1) Если принять в качестве переменной интегрирования 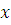,то

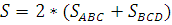, где

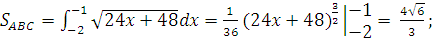
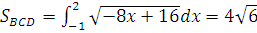, следовательно,

;

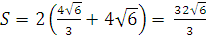2)Если принять в качестве переменной интегрирования , то ,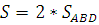

где 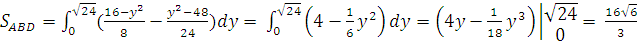, следовательно, .

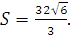Отметим, что в первом варианте расчета площади приходится разбивать фигуру 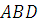на две: 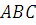и 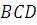, поскольку верхняя граница области состоит из двух различных фрагментов. Во втором варианте такой необходимости нет, так как фигура 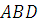имеет единую левую и правую границы.

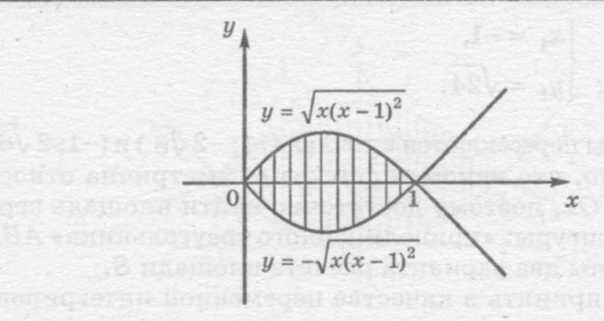
в) Целесообразно хотя бы эскизно воспроизвести график функции 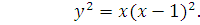Данная линия образует петлю, которая симметрична относительно оси следовательно,

.

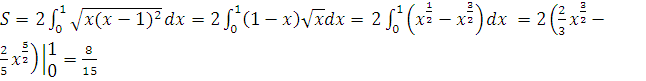Здесь учтено, что при 0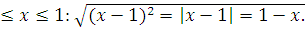

Ответ: а)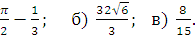

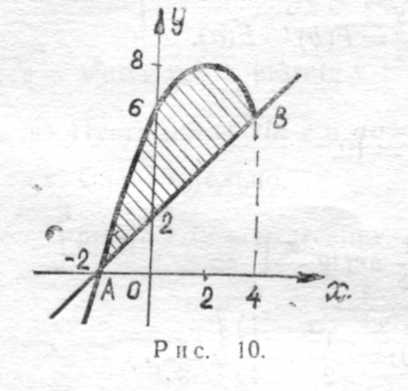
г) Вычислить площадь фигуры, ограниченной параболой y=2x- 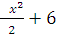и прямой y= x+2. (рис. 10).

Решение:

Площадь фигуры, ограниченная сверху непрерывной кривой y=f(x), снизу – непрерывной кривой y= 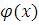, слева – прямой x=a и справа прямой x=b, вычисляется по формуле

S= 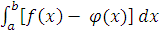(1)

В тех случаях, когда заданные кривые образуют замкнутую область, и прямые x=a и x=b не заданы, то числа a и b совпадают с абсциссами точек пересечения кривых. Находим точки пересечения заданных линий. Для этого решаем совместно систему уравнений

y=2x -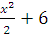

y= x+2

x+2=2x- 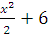; 2x+4=4x- ; ;

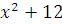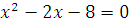откуда 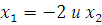=4; следовательно, a=-2 и b=4. Парабола и прямая пересекаются в точках А(-2;0) и В(4;6). Применяя (1), имеем:

S=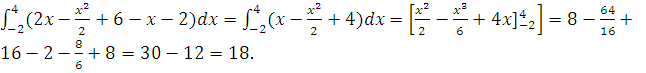

Следовательно, искомая площадь S=18 кв.ед.