Инвестиции в В 5 страница

галлонов,

(3)

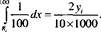
Из последнего уравнения имеем

Л, = 100-—. 50

Теперь используем уравнения (3) и (4), чтобы найти решение.

(4)

Итерация 1.

Л, =100-

316.23 50

= 93,68 галлонов.

Глава 16. Вероятностные модели управления запасами

Итерация 2.

R¹

S = —!—R. +50 = 0,19971 галлонов. 200

у_г = Vl00000 +10000 х0,19971=319,37 галлонов.

Следовательно,

Л, =100---— = 93,612 галлонов.

² 50

Итерация 3.

R²

S = —^— Л, + 50 = 0,20399 галлонов. 200

у, = ^100000 +10000 х 0,20399 =319,44 галлонов.

Следовательно,

319 44

Л, =100---— = 93,611 галлонов.

³ 50

Поскольку значения R₂ и R₃ примерно одинаковы, приближенное оптимальное ре­шение определяется значениями Л* ж 93,61 галлонов, 319,4 галлонов. Следова­тельно, оптимальное управление запасами состоит в размещении заказа примерно на 320 галлонов, как только запас уменьшается до 94 галлонов.

На рис. 16.4 показаны эти же вычисления, выполненные в шаблоне Excel chl6ContinuousReviwModel.xls. Здесь задана высокая точность вычислений 0,000001 (в ячейке С8) только для того, чтобы продемонстрировать скорость сходимости ал­горитма. На практике такая высокая точность не требуется. Шаблон рассчитан только на равномерное распределение спроса.

	В	С	D	E
	Continuous Review Model
	Input data: _
	Demand rate, D =	1000 ■
	Setuo cost, К =
	Unit holding cost, h	21
	Unit penalty cost, p=	10|
	Uniform limits(a. b)=		^^^iao]
	Tolerance =	0.0000011
	Optimum solution:
	Order quantity, y* =	319 438282
	Reorder point, R* =	93 611234
	Total expected cost =	826.10
	iteratvie calculations:
	Iteration i	yi	Ri	Si
		316.227766	0.000000	0 000000
		316 227766	93 675445	0.200000
17 18		319 374388	93.612512	0.204000
	319.437005	93.611260	0.204080
		319.438257	93 611235	0.204082
		319 438282	93.611234	0.204082

Рис. 16.4. Реализация в Excel вычислений примера 16.1.2

16.2. Одноэтапные модели

УПРАЖНЕНИЯ 16.1.2

1. Для данных, приведенных в примере 16.1.2, определите следующее.

a) Приближенное число заказов в месяц.

b) Ожидаемое значение месячной стоимости размещения заказов.

c) Ожидаемое значение месячных затрат на хранение.

d) Ожидаемое значение месячных затрат, связанных с дефицитом.

e) Вероятность истощения запаса в течение периода выполнения заказа.

2. Решите задачу из примера 16.1.2, учитывая, что спрос в период выполнения заказа является случайной величиной, равномерно распределенной на ин­тервале [0, 50] (галлонов).

3. В задаче из примера 16.1.2 предположите, что спрос в период поставки явля­ется случайной величиной, равномерно распределенной на интервале [40, 60] (галлонов). Сравните решение, полученное при этих условиях, с решением, полученным в примере 16.1.2, и интерпретируйте результаты. (Подсказка. В обеих задачах величина М{х) одинакова, но дисперсия в этой задаче меньше.)

4. Найдите оптимальное решение задачи из примера 16.1.2, если спрос в период поставки является нормально распределенной случайной величиной со сред­ним 100 галлонов и стандартным отклонением 2 галлона. Предположите также, что D = 10000 галлонов в месяц, Л = 2 долл. за галлон в месяц, р = 4 долл. за галлон и К = 20 долл.

16.2. ОДНОЭТАПНЫЕ МОДЕЛИ

Одноэтапные модели управления запасами отражают ситуацию, когда для удовле­творения спроса в течение определенного периода продукция заказывается только один раз. Например, модный сезонный товар устаревает к концу сезона, и, следовательно, заказы на него могут не возобновляться. В данном разделе рассматривается два типа таких моделей: с учетом и без учета затрат на оформление заказов.

При изложении данного материала используются следующие обозначения.

с — стоимость закупки (или производства) единицы продукции,

К — стоимость размещения заказа,

h — удельные затраты на хранение единицы продукции в течение рассматри­ваемого периода,

р — удельные потери от неудовлетворенного спроса (на единицу продукции за рассматриваемый период),

D — величина случайного спроса за рассматриваемый период,

f(D) — плотность вероятности спроса за рассматриваемый период,

у — объем заказа,

х — наличный запас продукта перед размещением заказа.

Модель определяет оптимальный объем заказа у, который минимизирует сум­марные ожидаемые затраты, связанные с закупкой (или производством), хранени­ем и неудовлетворенным спросом. При известном оптимальном значении у (обозна­чается у') оптимальное управление запасами состоит в размещении заказа объемом у" - х, если х < у; в противном случае заказ не размещается.

Глава 16. Вероятностные модели управления запасами

16.2.1. Модель при отсутствии затрат на оформление заказа

В этой модели принято следующее.

1. Спрос удовлетворяется мгновенно в начале периода непосредственно после получения заказа.

2. Затраты на размещение заказа отсутствуют.

На рис. 16.5 иллюстрируется состояние запаса после удовлетворения спроса D. Если D <у, запас у-D хранится на протяжении периода. Если жеD> у, возникает дефицит объема D - у.

У ♦

D<y

D

У

±

D-y

Т

D>y

-Время

б

Рис. 16.5. Состояние запаса в одноэтапной модели Ожидаемые затраты М{С(у)} на период выражаются следующей формулой.

М {С(у)} = с(у - х) + h)(у - D)f(D)dD + p](D - y)f{D)dD.

О v

Можно показать, что функция М{С(у)} является выпуклой по у и, таким образом, имеет единственный минимум. Следовательно, вычисляя первую производную функции М{С(у)} по у и приравнивая ее к нулю, получим

c + h)f{D)dD-p]f(D)dD = 0

О V

или

с + hP{D <у}+ р(1 - P{D < у}) = 0.

Отсюда имеем

P{D<y'} =

Р-С p + h

Правая часть последней формулы известна как критическое отношение. Значение у определено только при условии, что критическое отношение неотрицательно, т.е. р > с. Ситуация, когда р < с, является бессмысленной, так как это предполагает, что стоимость закупки единицы продукции выше потери от неудовлетворенного спроса.

Ранее предполагалось, что спрос D является непрерывной случайной величи­ной. Если же D является дискретной величиной, то плотность распределения веро­ятностей /(£>) определена лишь в дискретных точках и функция затрат вычисляет­ся в соответствии с формулой

M{C{y)} = c(y-x) + h^(y~D)f(D) + p J (D-y)f(D).

Необходимыми условиями оптимальности служат неравенства М{С(у - 1)} > М{С(у)} и М{С(у + 1)} > М{С(у)}.

16.2. Одноэтапные модели

Эти условия в данном случае являются достаточными, так как функция М{С(у)} выпукла. Применение этих условий после некоторых алгебраических преобразова­ний приводит к следующим неравенствам для определения у'.

P{D </-!}< <P{D< у'}.

Пример 16.2.1

Владелец газетного киоска должен определить количество экземпляров газеты USA Now, которые должны быть в продаже в начале каждого дня. Он покупает экземп­ляр газеты за 30 центов, а продает за 75 центов. Продажа газеты обычно происхо­дит с 7.00 до 8.00 часов утра. Оставшиеся к концу дня экземпляры газеты повторно выставляются для продажи по цене 5 центов за экземпляр. Сколько экземпляров газеты должен закупить владелец каждое утро, если дневной спрос описывается одним из следующих вероятностных распределений.

1. Нормальным распределением с математическим ожиданием 300 экземпляров и стандартным отклонением 20 экземпляров.

2. Дискретной плотностью распределения/^), заданной в виде следующей таблицы.

D
т	0,1	0,2	0,4	0,2	0,1

Стоимости хранения и потери, обусловленные дефицитом, в этой ситуации не оп­ределены в явном виде. Однако данные задачи свидетельствуют о том, что каждый непроданный экземпляр газеты обходится владельцу в 30 - 5 = 25 центов, и что по­тери, связанные с истощением запаса газет, равны 75 - 30 = 45 центов за экземп­ляр. Следовательно, в терминах, принятых в модели управления запасами, мы мо­жем предполагать, что с = 30 центов за экземпляр, И = 25 центов за экземпляр, р = 45 центов за экземпляр в день.

Сначала определяем критическое отношение

^£ = ^ = 0,2.4. p + h 45 + 25

Ситуация 1. Спрос D распределен по нормальному закону /V(300, 20). Определим стандартную нормально распределенную случайную величину (с законом распре­деления N(0, 1))

D-300

Из таблицы стандартного нормального распределения находим (см. приложение В)

P{z< -0,79} = 0,214.

Тогда

^00=-0,79. 20

Следовательно, оптимальный объем заказа равен у* = 284,2 (или примерно 284) эк­земпляров.

Глава 16. Вероятностные модели управления запасами

Ситуация 2. Спрос D описывается дискретной плотностью распределения ДО). Сна­чала найдем функцию распределения Р{ D < у}.

У
Р{0<у}	0,1	0,3	0,7	0,9	1,0

Для вычисленного критического отношения 0,214 имеем неравенства

P{D < 200} < 0,214 < P{D < 220}. Отсюда следует, что у" = 220 экземпляров.

УПРАЖНЕНИЯ 16.2.1

1. Покажите, что для одноэтапной модели с дискретной величиной спроса оп­тимальный объем заказа определяется из соотношения

2. Спрос на продукцию в течение единственного периода удовлетворяется мгно­венно в начале периода. Соответствующая плотность распределения вероят­ностей является экспоненциальной со средним 10 единиц. В силу сложности оценки стоимостных параметров объем заказа определяется таким образом, что вероятность либо излишка, либо дефицита не превышает 0,1. Можно ли удовлетворить оба условия одновременно?

3. В одноэтапной модели управления запасами стоимость закупки единицы про­дукции равна 10 долл., а стоимость ее хранения— 1долл. Найдите допусти­мую область значений удельных потерь от неудовлетворенного спроса в опти­мальном случае, если объем заказа равен 4 единицы. Также предполагается, что спрос удовлетворяется мгновенно в начале периода, и что плотность рас­пределения величины спроса представляется следующей таблицей.

D
т	0,05	0,1	0,1	0,2	0,25	0,15	0,05	0,05	0,05

4. Книжный магазин университета предлагает ксерокопии конспектов лекций университетских профессоров. Профессор Ятаха читает лекции первокурс­никам; на первый курс принимается от 200 до 250 студентов, причем ожи­даемое количество первокурсников подчиняется равномерному распределе­нию. Изготовление каждой копии обходится в 10 долл., магазин продает их студентам по 25 долл. за копию. Студенты покупают конспекты в начале се­местра. Каждая непроданная копия конспекта профессора Ятахи выставля­ется для продажи по частям. Между тем, если в магазине заканчиваются ко­пии конспектов, дополнительные копии не печатаются, и студенты сами заботятся о том, чтобы достать конспекты из других источников. Сколько копий конспектов лекций следует напечатать магазину, если он заинтересо­ван в максимизации своих доходов?

5. Магазин быстрого обслуживания предлагает посетителям кофе и орехи с шести часов утра каждый день. Магазин покупает орехи по 7 центов за порцию,

16.2. Одноэтапные модели

а продает по 25 центов за порцию до 8 часов утра. После этого времени орехи продаются по 5 центов за порцию. Число посетителей, которые ежедневно по­купают орехи, является случайной величиной, равномерно распределенной на интервале [30, 50]. Каждый посетитель обычно заказывает три порции орехов с кофе. Сколько примерно порций орехов следует закупать магазину каждое утро в целях максимизации своих доходов?

6. Магазин одежды создает запас теплых пальто для приближающейся зимы. Каждое пальто закупают по 50 долл., а продают со 100% -ной наценкой. В кон­це сезона проводится распродажа, и пальто реализуется по цене 55 долл. Спрос на пальто в течение зимнего сезона является случайной величиной, равномер­но распределенной на интервале от 20 до 30. Так как зимний сезон является коротким, затраты на хранение в расчет не принимаются. Управляющий мага­зина считает также, что не будет потерь, вызванных дефицитом товара. Опре­делите оптимальный объем заказа, который максимизирует доходы магазина.

7. Пусть в рамках одноэтапной модели спрос в течение периода меняется равно­мерно (а не удовлетворяется мгновенно в начале периода). Разработайте соот­ветствующую стоимостную модель и определите оптимальный объем заказа.

8. Решите задачу из примера 16.2.1, предположив, что спрос непрерывен и рав­номерен в течение периода; плотность вероятности спроса является постоянной на интервале от 0 до 100. (Совет. Воспользуйтесь результатами упражнения 7.)

16.2.2. Модель при наличии затрат на оформление заказа

Рассматриваемая модель отличается от представленной в предыдущем разделе тем, что учитывается стоимость К размещения заказа. Используя обозначения, введенные выше, получаем следующее выражение для суммарной ожидаемой стоимости.

Как показано в разделе 16.2.1, оптимальное значение у' должно удовлетворять соотношению

Так как К является константой, минимум величины М{С(у)} также должен дости­гаться при у', как показано на рис. 16.6.

М[С{у)} = К + М{С(у) } = K + c{y-x) + h\(y-D)f(D)dD +p\(D- y)f(D)dD.

Заказывать

He заказывать

Рис. 16.6. Определение оптимальной ве­личины заказа

Глава 16. Вероятностные модели управления запасами

На рис. 16.6 S = у и величина s (< S) определяются из уравнения

M{C(s)} = M{C(S)\=K + M{C(S)}, s<S.

(Отметим, что это уравнение имеет и другое решение s, > S, которое не рассмат­ривается.)

Задача формулируется следующим образом. Какое количество продукции необ­ходимо заказывать, если наличный запас перед размещением заказа составляет х единиц? Ответ на этот вопрос рассматривается по отдельности при выполнении следующих условий.

1. x<s.

2. s<x<S.

3. x>S.

Ситуация 1 (х < s). Так как в наличии имеется х единиц продукции, соответст­вующие издержки содержания запаса составляют М{С(х)}. Если заказывается лю­бое дополнительное количество продукции у - х (у > х), то соответствующие затра­ты при заданной величине у равны величине М{С(у)}, которая учитывает стоимость К размещения заказа. Из рис. 16.6 следует, что

min М {С(у)} = М {C(S)} < М {С(х)}.

Следовательно, оптимальной стратегией управления запасами в этом случае будет заказ bS - х единиц.

Ситуация 2 (s < х < S). Из рис. 16.6 видно, что

M{C(x)}<mmM{C(y)) = M{C(S)}.

Следовательно, в данном случае дополнительных затрат не возникает, если новый заказ не размещается. Поэтому у = х.

Ситуация 3 (х > S). Из рис. 16.6 видно, что при у > х

М{С(х))<М{С(у)}.

Это неравенство показывает, что в данном случае экономнее будет не размещать за­каз, т.е. у" = х.

Описанная стратегия управления запасами, часто именуемая (з-5)-стратегией, определяется следующим правилом.

Если х < s, делать заказ объемом S - х,

если х > s, заказывать не следует.

Оптимальность (я-5)-стратегии следует из того, что соответствующая функция затрат является выпуклой. Если это свойство не выполняется, данная стратегия перестает быть оптимальной.

Пример 16.2.2

Дневной спрос на продукцию в течение одного периода удовлетворяется мгно­венно в начале периода. Спрос является случайной величиной, равномерно распределенной от 0 до 10 единиц. Стоимость хранения единицы продукции на протяжении периода равна 0,50 долл., а штраф за дефицит единицы продук­

16.2. Одноэтапные модели

ции— 4,50 долл. Стоимость единицы продукции равна 0,50 долл., стоимость размещения заказа — 25 долл. Необходимо определить оптимальную страте­гию заказа продукции.

Определим сначала у. Имеем

р-с 4,5-0,5

= 0.8.

Так как

p + h 4,5 + 0,5

p{D<y}= \±<Ю=У-

¹ ' ho if

ю

то S = у =8.

Ожидаемое значение функции затрат определяется следующим образом.

M{C{y)} = Q.5{y-x) + Q.5\^{y-D)dD + 4,s)^{D-y)dD =

= 0,25r-4;y + 22,5-0.5x Величина s определяется из уравнения

M{C(s)} = K + M{C(S)}.

Отсюда получаем

0,25Г - 4s + 22,5 - 0,5* = 25 + 0,255² - 45 + 22,5 - 0,5*. При 5 = 8 это уравнение сводится к виду

/-16л-36 = 0.

Решением данного уравнения является s = -2 и 5=18. Значение 5 = 18 (превы­шающее 5) следует отбросить. Так как оставшееся значение является отрицатель­ным (= -2), то s не имеет допустимого значения. Следовательно, оптимальной стра­тегией является отказ от размещения заказа (рис. 16.7). Такая ситуация обычно возникает тогда, когда функция затрат является "плоской" или когда затраты на размещение заказа превышают другие затраты модели.

М{С(е)}

Рис. 16.7. Оптимальная стратегия размещения заказа для примера 16.2.2

Глава 16. Вероятностные модели управления запасами

УПРАЖНЕНИЯ 16.2.2

1. Определите оптимальную стратегию управления запасами для ситуации, описанной в примере 16.2.2, если предположить, что стоимость размещения заказа составляет 5 долл.

2. Пусть в одноэтапной модели, рассмотренной в разделе 16.2.1, необходимо максимизировать прибыль, при этом следует учитывать стоимость размеще­ния заказа К. Постройте формулу для ожидаемого значения прибыли и опре­делите оптимальный объем заказа, используя при этом информацию из раз­дела 16.2.1 и предполагая, что стоимость продажи единицы продукции равна г. Решите задачу при следующих данных (все величины в долл.): г= 3, с = 2, р = 4, h = 1 w. К = 10. Плотность вероятности спроса является постоянной на интервале [0, 10].

3. Решите упражнение 16.2.1.5, предполагая, что доставка орехов связана с по­стоянными затратами в 10 долл.

16.3. МНОГОЭТАПНЫЕ МОДЕЛИ

В этом разделе рассматривается многоэтапная модель без учета стоимости размещения заказа. Кроме того, в модели предусматривается возможность за­долженности и нулевое время поставки. Предполагается также, что спрос D в каждый период описывается стационарной (независящей от времени) плотно­стью вероятности /(£>).

В многоэтапной модели учитывается приведенная стоимость денег. Если or(< 1) — коэффициент дисконтирования (процент скидки) для одного этапа, то сумма А спустя п этапов будет эквивалентна сумме dA в настоящий момент.

Предположим, что планирование охватывает п этапов, и неудовлетворенный спрос может оставаться таковым лишь на протяжении одного этапа. Пусть F_t(x_t) — максимальная суммарная ожидаемая прибыль для этапов от i до п, определенная при условии, что x_t — уровень имеющегося запаса перед размещением заказа на t-м этапе.

Используя обозначения из раздела 16.2 и предполагая, что г— удельный доход от реализации единицы продукции, сформулируем задачу управления запасами в виде следующей задачи динамического программирования (см. главу 15).

F,(лс,) = тах{-с(у, -х,)+ j[rD-й(у, - D)]f{D)dD +

+)[ry_i+ar(D-y_i)-p{D~y_i)]f(D)clD +

+ a\F_M{_yi-D)f{D)dD), i = 1.2.....л,

о

где F„_+/(j/„ - D) = 0. Величина x_t может принимать отрицательные значения, так как неудовлетворенный спрос может накапливаться. Величина ar(D - у) включена во второй интеграл, поскольку D- y_t представляет собой неудовлетворенный спрос на t-м этапе, который должен быть удовлетворен на этапе i + 1.

Задачу можно решить рекуррентно методами динамического программирова­ния. Если число этапов является бесконечным, приведенное выше рекуррентное уравнение сводится к следующему.

16.3. Многоэтапные модели

F(x) = ma.x[-c(y-x) + §_rD-h(y-D)]f(D)dD +

^{у Л} О

+ \ry + ar{D-y)-p(D~y)]f(D)dD +

У

+ aJF(y-D)f(D)dD},

о

где х и у представляют собой уровни запаса на каждом этапе до и после получения заказа соответственно.

Оптимальное значение у можно определить из приведенного ниже необходимого условия, которое в данном случае есть также достаточным, так как функция ожи­даемой прибыли F(x) является вогнутой.

^ = -c-h)f{D)dD + \{l-a)r+ _P]f{D)dD + af^F^~^D^f(D)dD = 0.

Эу о v о ду

dF(y-D)

Величина —--- определяется следующим образом. Если на начало следующего

Эу

этапа уровень запаса еще составляет /?(>0) единиц, то прибыль на этом этапе воз­растает на величину cj3, так как объем последующего заказа уменьшается именно на эту величину. Это означает, что

dF(y-D) _

Следовательно, необходимое условие принимает вид

у (V \

-c-hjf(D)dD + [(l-a)r+p] \-\f{D)dD +oxjf{D)dD = 0.

о V о у о

Поэтому оптимальный уровень заказа у* определяется из уравнения

р + (\-а)(г-с)

\f{D)dD-.

p + h + (\-a)r

Оптимальная стратегия каждого этапа при заданном исходном запасе д: выра­жается следующим правилом.

Если л: < у*, делать заказ объемом у - х, если х>у, заказа не делать.

УПРАЖНЕНИЯ 16.3

1. Рассмотрим двухэтапную вероятностную модель управления запасами, в ко­торой спрос накапливается, а заказы поступают с нулевым запаздыванием. Спрос в каждый период описывается постоянной плотностью вероятности на интервале от 0 до 10. Стоимостные параметры модели таковы: цена продажи единицы продукции — 2 долл., цена покупки единицы продукции — 1 долл., стоимость хранения единицы продукции — 0,10 долл., штраф за дефицит единицы продукции — 3 долл., коэффициент дисконтирования — 0,8.

Глава 16. Вероятностные модели управления запасами

Определите оптимальную стратегию для двух этапов, предполагая, что на­чальный запас для первого периода равен нулю.

2. Плотность распределения величины спроса для каждого этапа в модели управле­ния запасами при бесконечном горизонте планирования имеет вид f(D) = 0,08Д О < D < 5. Стоимостные параметры, отнесенные к единице продукции, таковы:

цена продажи — 10 долл.,

цена покупки — 8 долл.,

штраф за дефицит — 1 долл.,

коэффициент дисконтирования — 0,9.

Определите оптимальную стратегию управления запасами, предположив, что заказы выполняются с нулевым запаздыванием и неудовлетворенный спрос накапливается.

3. Дана модель управления запасами при бесконечном горизонте планирования, в которой заказы выполняются с нулевым запаздыванием, а неудовлетво­ренный спрос накапливается. Определите оптимальную стратегию управле­ния запасами, основанную на минимизации ожидаемых затрат, если

затраты на хранение г единиц продукции — hz\

штраф за дефицит z единиц продукции — рг².

Покажите, что в частном случае, когда h= р, оптимальное решение не зави­сит от конкретного вида вероятностного распределения спроса.

ЛИТЕРАТУРА

1. Hadley G. and Whitin Т., Analysis of Inventory Systems, Prentice Hall, Upper Saddle River, N. J., 1963. (Русский перевод: Хедли Дж., Уайтин Т. Анализ систем управления запасами. — М.: Наука, 1969.)

2. Silver Е. and Peterson R. Decision Systems for Inventory Management and Produc­tion Planning, 2nd ed., Wiley, New York, 1985.

3. Tersine R. Principles of Inventory and Materials Management, North Holland, New York, 1982.

Литература, добавленная при переводе

1. Кофман А. Методы и модели исследования операций. — М.:Мир, 1966.

2. Мур Дж., Уэдерфорд Л. Экономическое моделирование в Microsoft Excel. — М.: Издательский дом "Вильяме", 2004.

КОМПЛЕКСНЫЕ ЗАДАЧИ

16.1. ² Телефонная компания управляет телефонными центрами, которые пре­доставляют услуги клиентам по месту жительства в своих регионах. Суще­ствует более 60 моделей телефонных аппаратов, которые предлагаются

Этот пример взят из работы Cohen R. and Dunford F. "Forecasting for Inventory Control: An Example of When "Simple" Means "Better", Interfaces, Vol. 16, No. 6, pp. 95-99, 1986.

Комплексные задачи

клиентам. В настоящее время каждый телефонный центр содержит запас телефонных аппаратов, рассчитанный на срок от 15 до 75 дней. Управляю­щий считает такие уровни запаса чрезмерными, так как они ежедневно по­полняются из центрального товарного склада. В то же время управляющий должен гарантировать, что в телефонных центрах поддерживается уровень запаса, достаточный для обеспечения обслуживания клиентов на уровне 95 %. Изучающий проблему коллектив специалистов начал свою работу со сбора соответствующих данных. Задача этого коллектива — определить оп­тимальный уровень запаса для каждой модели телефонного аппарата. Сле­дующая таблица содержит количество установленных за день настольных телефонных аппаратов зеленого цвета с вращающимся наборным диском.

Установленные аппараты
Частота

Аналогичные таблицы были построены для всех моделей телефонных ап­паратов.

Стоимостные параметры, необходимые для определения оптимального уровня запаса каждой модели телефонного аппарата, трудно поддаются оценке, и, следовательно, применение традиционных моделей управления запасами невозможно. Поэтому исследовательский коллектив решил ис­пользовать более основательный подход к определению соответствующего уровня запаса для различных моделей телефонных аппаратов. В результате исследования был сделан вывод, что как регрессионный анализ, так и ана­лиз временных рядов не смогли обнаружить заметных тенденций спроса.

Предложите метод определения соответствующих уровней запаса для раз­личных моделей телефонных аппаратов. Сформулируйте все предположе­ния, необходимые для получения решения.

16.3. ³ Менеджер по снабжению небольших магазинов розничной торговли раз-» мещает заказы на продукцию, чтобы получить выгоду за счет специаль­ных цен или объединения заказов, полученных от одного поставщика. В результате как объем заказа, так и продолжительность цикла (период между последовательными заказами) являются случайными. Более то­го, поскольку стратегия менеджера, в основном, определяется не сооб­ражениями управления запасами, объем заказа и продолжительность цикла могут рассматриваться независимо в том смысле, что из меньшей длительности циклов не следует (с необходимостью) меньший объем зака­зов и наоборот.

Приведенная ниже таблица содержит типичные данные для трех наиме­нований продукции, которые были заказаны одновременно. Эти данные показывают, что как объем заказа, так и продолжительность цикла яв­ляются случайными величинами. Более того, даже беглый анализ данных таблицы обнаруживает отсутствие корреляции между объемом заказа и продолжительностью цикла.