Промежуточные вычислении 13 страница

Глава 9. Целочисленное линейное программирование

Компания ABC собирается выбрать три или четыре рекламных центра. Где они должны быть расположены?

9.4. ⁶ Электрическая компания, обслуживающая сельские районы, хочет опреде­лить количество своих сервисных центров и их местоположение. Компания об­служивает 5 районов, в которых проживает следующее число потребителей.

Район
К-во потребителей

Компания определила пять возможных мест для размещения своих сервис­ных центров. В следующей таблице приведены средние расстояния от этих возможных центров до районов потребления.

Сервисный центр

Район

Средняя скорость передвижения аварийных машин сервисных центров со­ставляет 45 миль в час. Компания хочет, чтобы пользователи в любом рай­оне ожидали аварийные машины не более 90 минут. Где должны распола­гаться сервисные центры?

⁶ Задача основана на материалах статьи Erkut Е., Myrdon Т., Strangway К. "Transatlanta Redesigns Its Service Delivery Network", Interfaces, Vol.30, No. 2, 2000, pp. 54-69.

ГЛАВА 10

ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ

ДИНАМИЧЕСКОГО

ПРОГРАММИРОВАНИЯ

Динамическое программирование (ДП) определяет оптимальное решение п-мерной задачи путем ее декомпозиции на п этапов, каждый из которых представ­ляет подзадачу относительно одной переменной. Вычислительное преимущество такого подхода состоит в том, что мы занимаемся решением одномерных оптими­зационных подзадач вместо большой л-мерной задачи. Фундаментальным принци­пом ДП, составляющим основу декомпозиции задачи, является оптимальность. Так как природа каждого этапа решения зависит от конкретной оптимизационной задачи, ДП не предлагает вычислительных алгоритмов непосредственно для каж­дого этапа. Вычислительные аспекты решения оптимизационных подзадач на ка­ждом этапе проектируются и реализуются по отдельности (что, конечно, не исклю­чает применения единого алгоритма для всех этапов).

10.1. РЕКУРРЕНТНАЯ ПРИРОДА ВЫЧИСЛЕНИЙ ДП

Вычисления в ДП выполняются рекуррентно в том смысле, что оптимальное решение одной подзадачи используется в качестве исходных данных для следую­щей. Решив последнюю подзадачу, мы получим оптимальное решение исходной задачи. Способ выполнения рекуррентных вычислений зависит от того, как произ­водится декомпозиция исходной задачи. В частности, подзадачи обычно связаны между собой некоторыми общими ограничениями. Если осуществляется переход от одной подзадачи к другой, то должны учитываться эти ограничения.

Пример 10.1.1. Задача о кратчайшем пути

Предположим, необходимо выбрать кратчайший путь между двумя городами. Сеть дорог, показанная на рис. 10.1, представляет возможные маршруты между исходным городом, находящимся в узле 1, и конечным пунктом, который нахо­дится в узле 7. Маршруты проходят через промежуточные города, обозначенные на сети узлами с номерами 2-6.

Глава 10. Детерминированные модели динамического программирования

Старт м

Рис. 10.1. Сеть дорог для примера 10.1.1

Мы можем решить эту задачу посредством полного перебора всех маршрутов меж­ду узлами 1 и 7 (имеется пять таких маршрутов). Однако в большой сети полный перебор является неэффективным с вычислительной точки зрения.

Чтобы решить эту задачу с помощью методов динамического программирования, сна­чала разделим ее на этапы. Вертикальные пунктирные линии на рис. 10.2 очерчивают три этапа задачи. Далее выполняются вычисления для каждого этапа в отдельности.

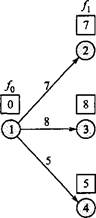
Рис. 10.2. Декомпозиция задачи на три этапа

Общая задача состоит в вычислении кратчайших (постепенно накапливаемых) рас­стояний ко всем вершинам этапа с последующим использованием этих расстояний в качестве исходных данных для следующего этапа. Рассматривая узлы, относящиеся к первому этапу, замечаем, что каждый из узлов 2, 3 и 4 связан с начальным узлом 1 единственной дугой (рис. 10.2). Следовательно, для первого этапа имеем следующее.

Этап 1. Итоговые результаты.

Кратчайший путь к узлу 2 равен 7 миль (из узла 1).

Кратчайший путь к узлу 3 равен 8 миль (из узла 1).

Кратчайший путь к узлу 4 равен 5 миль (из узла 1).

Далее переходим ко второму этапу для вычисления кратчайших (накопленных) расстояний к узлам 5 и 6. Рассматривая узел 5 первым, из рис. 10.2 замечаем, что

10.1. Рекуррентная природа вычислений ДП

есть три возможных маршрута, по которым можно достичь узла 5, а именно (2, 5), (3, 5) и (4, 5). Эта информация вместе с кратчайшими расстояниями к узлам 2, 3, и 4 определяет кратчайшее (накопленное) расстояние к узлу 5 следующим образом.

Кратчайший

I = min

_чпуть к узлу 5 I ''=2.з.4

Кратчайший "\ (Расстояние от ^путь к узлу i J yysna / к узлу 5, 7 + 12 = 19

8+ 8 = 16 5+ 7 = 12

Аналогично для узла 6 имеем следующее.

Кратчайший ^ \(Кратчайший

= тЫ

путь к узлу 6) '=^{3 4} И путь к узлу i

-12 (изузла4).

Расстояние от _чузла (' к узлу 6

S+ 9 = 17:min<? = 17 (изузла3).

15+ 13 = 18' ¹ '

Этап 2. Итоговые результаты.

Кратчайший путь к узлу 5 равен 12 миль (из узла 4).

Кратчайший путь к узлу 6 равен 17 миль (из узла 3).

Последним шагом является третий этап. Конечный узел 7 можно достичь как из узла 5, так и 6. Используя итоговые результаты этапа 2 и расстояния от узлов 5 и 6 к узлу 7, получаем следующее.

'Кратчайший⁴ путь к узлу 1 _/

12 + 9 = 21:min() = 21 (из узла 5).

17 + 6 = 23' ^{V У} '

Этап 3. Итоговые результаты.

Кратчайший путь к узлу 7 равен 21 миле (из узла 5).

Приведенные вычисления показывают, что кратчайшее расстояние между узлами 1 и 7 равно 21 миле. Города, через которые проходит кратчайший маршрут, опре­деляются следующим образом. Из итоговых результатов третьего этапа следует, что узел 7 связывается с узлом 5. Далее из итоговых результатов второго этапа сле­дует, что узел 4 связывается с узлом 5. Наконец, из итоговых результатов первого этапа следует, что узел 4 связывается с узлом 1. Следовательно, оптимальным маршрутом является последовательность 1—> 4-* 5-* 7.

Теперь покажем, как рекуррентные вычисления динамического программиро­вания можно выразить математически. Пусть Дх,-) — кратчайшее расстояние до уз­ла х, на этапе /, d(x_Lljci) — расстояние от узла до узла дг,. Тогда / вычисляется на основе значений f_Ll с помощью следующего рекуррентного уравнения.

/(*,)= min {«/(*,_,,*,) + /-.(*,-.)}. 1 = 1.2,3.

все допустимые ^{L 1} {^xi-\-^xi)-маршругы

При /' = 1 полагаем /₀(*₀) = 0. Это уравнение показывает, что кратчайшие расстояния /(дг,) на этапе / должны быть выражены как функции следующего узла дг,. В термино­логии динамического программирования дг, именуется состоянием системы на этапе /.

Глава 10. Детерминированные модели динамического программирования

В действительности состояние системы на этапе i— это информация, связывающая этапы между собой, при этом оптимальные решения для оставшихся этапов могут при­ниматься без повторной проверки того, как были получены решения на предыдущих этапах. Такое определение состояния системы позволяет рассматривать каждый этап отдельно и гарантирует, что решение является допустимым на каждом этапе.

Определение состояния системы приводит к следующему унифицированному положению.

Принцип оптимальности. На каждом этапе оптимальная стратегия определяет­ся независимо от стратегий, использованных на предыдущих этапах.

Применение принципа оптимальности демонстрируется вычислениями из при­мера 10.1.1. Например, на этапе 3 мы используем кратчайшие пути к узлам 5 и 6 и не интересуемся, как эти узлы были достигнуты из узла 1.

УПРАЖНЕНИЯ 10.1

1. Решите задачу из примера 10.1.1, предполагая, что используются следую­щие длины маршрутов:

d(l, 2) = 5,^(1,3) = 9,^(1,4) = 8,

d(2, 5)= 10, d(2, 6)= 17,

d(3, 5) = 4, d(3, 6)= 10,

d(4, 5) = 9, d(4, 6) = 9,

d(5, 7) = 8,

d(6,1) = 9.

2. Я — заядлый турист. Прошлым летом мы с другом отправились в пятиднев­ный поход по прекрасным Белым Горам в штате Нью-Гемпшир. Мы решили ограничить наше путешествие территорией, на которой расположены три хорошо известные вершины: Вашингтон, Джефферсон и Адаме. Гора Ва­шингтон имеет шестимильную тропу от подножия до вершины. Аналогич­ные тропы гор Джефферсона и Адамса имеют длину 4 и 5 миль соответствен­но. Тропы, соединяющие подножия этих трех гор, имеют следующую длину: 3 мили между вершинами Вашингтона и Джефферсона, 2 мили между вер­шинами Джефферсона и Адамса и 5 миль между вершинами Адамса и Ва­шингтона. В первый день мы стартовали от подножия вершины Вашингтона и вернулись в эту же точку к концу пятого дня. Нашей целью было пройти как можно более длинный путь. Мы также решили подниматься каждый день только на одну вершину и располагаться лагерем у подножия той горы, на которую мы решили восходить на следующий день. Кроме того, мы реши­ли, что не будем подниматься на одну и ту же вершину в течение двух дней подряд. Каким было расписание нашего похода?

10.2. РЕКУРРЕНТНЫЕ АЛГОРИТМЫ ПРЯМОЙ И ОБРАТНОЙ ПРОГОНКИ

В примере 10.1.1 вычисления проводились последовательно: от первого этапа до третьего. Такая последовательность вычислений известна как алгоритм прямой про­гонки. Этот же пример может быть решен с помощью алгоритма обратной прогонки, в соответствии с которым вычисления проводятся от третьего этапа до первого.

10.2. Рекуррентные алгоритмы прямой и обратной прогонки

Алгоритмы прямой и обратной прогонки приводят к одному и тому же реше­нию. Несмотря на то что алгоритм прямой прогонки представляется более логич­ным, в специальной литературе, посвященной динамическому программированию, неизменно используется алгоритм обратной прогонки. Причина этого в том, что в общем случае алгоритм обратной прогонки может быть более эффективным с вы­числительной точки зрения. Продемонстрируем использование алгоритма обрат­ной прогонки на примере 10.1.1. Мы также представим вычисления динамического программирования в компактной табличной форме.

Пример 10.2.1

Рекуррентное уравнение для алгоритма обратной прогонки в примере 10.1.1 имеет вид /(*,.)= min {d(x„x_M) + f_M{x_M)}, / = 1,2,3,

вес допустимые [x,.x,.i)-маршругы

где ffixj = 0 для x_t = 7. Соответствующей последовательностью вычислений будет

и-* и-* Л-

Этап 3. Поскольку узел 7 (x_t = 7) связан с узлами 5 и 6 (х₃ = 5 и 6) только одним маршрутом, альтернативы для выбора отсутствуют, а результаты третьего этапа можно подытожить следующим образом.

а\Х}, х₄) Оптимальное решение

Xi х₄ = 7 h(Xi) _x'_t

5 9 9 7

6 6 6 7

Этап 2. Так как маршрута (2, 6) не существует, соответствующая альтернатива не рассматривается. Используя значения f₃(x₃), полученные на третьем этапе, мы можем сравнить допустимые альтернативные решения, как показано в следующей таблице.

Хг	ф2, Хз) + 6(*з)	Оптимальное решение
Хз = 5	х3 = 6	«*) xl
	12 + 9 = 21	—	21 5
	8 + 9= 17	9 + 6 = 15	15 6
	7 + 9=16	13 + 6 = 19	16 5

Оптимальное решение второго этапа означает следующее. Если вы находитесь в уз­ле (городе) 2 или 4, кратчайший путь к узлу 7 проходит через узел 5, а если в узле

3 — через узел 6.

Этап 1. Из узла 1 начинаются три альтернативных маршрута: (1, 2), (1, 3) и (1, 4). Используя значения f₂(x₂), полученные на втором этапе, вычисляем данные сле­дующей таблицы.

Оптимальное решение на первом этапе показывает, что кратчайший путь проходит через город 4. Далее из оптимального решения на втором этапе следует, что из города

4 необходимо двигаться в город 5. Наконец, из оптимального решения на третьем этапе следует, что город 5 связан с городом 7. Следовательно, полным маршрутом, имеющим кратчайшую длину, является 1—> 4—> 5—> 7, и его длина равна 21 миле.

Глава 10. Детерминированные модели динамического программирования

		а\хи x2) + f2(x2)	Оптимальное решение
Х\	х2 = 2	х2 = 3 х2 = Л
	7 + 21 = 28	8 + 15 = 23 5 + 16 = 21	21 4

УПРАЖНЕНИЯ 10.2

1. Для задачи из упражнения 10.1.1 получите рекуррентное соотношение об­ратной прогонки и используйте его для получения оптимального решения.

2. Для задачи из упражнения 10.1.2 получите рекуррентное соотношение об­ратной прогонки и используйте его для получения оптимального решения.

3. Определите кратчайший маршрут между городами 1 и 7 на сети дорог, пред­ставленной на рис. 10.3. Определите этапы и состояния системы с помощью алгоритма обратной прогонки, а затем решите задачу.

Рис. 10.3. Сеть для упражнения 3

10.3. ПРИЛОЖЕНИЯ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ

В данном разделе рассмотрено четыре примера, каждый из которых выбран для демонстрации методов динамического программирования. При рассмотрении каж­дого примера особое внимание обратите на три основных элемента моделей дина­мического программирования.

1. Определение этапов.

2. Определение на каждом этапе вариантов решения (альтернатив).

3. Определение состояний на каждом этапе.

Из перечисленных выше элементов понятие состояния, как правило, представ­ляется весьма сложным для восприятия. Рассмотренные в этом разделе приложе­ния последовательно показывают, что определение состояния меняется в зависи­мости от моделируемой ситуации. При рассмотрении каждого приложения полезно ответить на следующие вопросы.

1. Какие соотношения связывают этапы вместе?

2. Какая информация необходима для того, чтобы получить допустимые реше­ния на текущем этапе без повторной проверки решений, принятых на преды­дущих этапах?

10.3. Приложения динамического программирования

Мой опыт преподавания показывает, что понятие состояния удается глубже уяснить, если поставить под сомнение определение состояния, которое предложено в настоящей книге. Рекомендуем воспользоваться каким-либо другим определени­ем, которое покажется вам "более логичным", и применить его в рекуррентных вычислениях. В конечном счете вы сможете убедиться, что приведенные здесь оп­ределения обеспечивают корректное решение задач. В то же время предложенный подход будет способствовать вашему пониманию самой концепции состояния.

10.3.1. Задача о загрузке

Задача о загрузке — это задача о рациональной загрузке судна (самолета, авто­машины и т.п.), которое имеет ограничения по объему или грузоподъемности. Ка­ждый помещенный на судно груз приносит определенную прибыль. Задача состоит в определении загрузки судна такими грузами, которые приносят наибольшую суммарную прибыль.

Перед тем как представить соотношения динамического программирования, заметим, что рассматриваемая здесь задача известна также как задача о снаряже­нии, где пилот реактивного самолета должен определить наиболее ценные (необходимые) предметы, которые следует взять на борт самолета, или как задача о рюкзаке, в которой солдат (или турист) должен определить наиболее ценные предметы, подлежащие загрузке в ранец (рюкзак). Кажется, что три упомянутых названия для одной и той же задачи были выбраны для того, чтобы гарантировать равное представительство военно-морского флота, воздушных сил и армии!

Рекуррентное уравнение процедуры обратной прогонки выводится для общей задачи загрузки судна грузоподъемностью W предметов (грузов) п наименований. Пусть т, — количество предметов £-го наименования, подлежащих загрузке, г,— прибыль, которую приносит один загруженный предмет /-го наименования, w,— вес одного предмета 1-го наименования. Общая задача имеет вид следующей цело­численной задачи линейного программирования.

Максимизировать z = г_хт_х + г₂т₂+... + г_пт„

при условии,что

иуи,+ w₂mi +... + w„m„< W, т_ь т₂,т„>0 и целые.

Три элемента модели динамического программирования определяется сле­дующим образом.

1. Этап i ставится в соответствие предмету /'-го наименования, i = 1,2,п.

2. Варианты решения на этапе i описываются количеством т, предметов /-го на­именования, подлежащих загрузке. Соответствующая прибыль равна гр\,. Зна­чение т,- заключено в пределах от 0 до [W/uv₍], где [W/wJ — целая часть числа W/w,.

3. Состояние х, на этапе i выражает суммарный вес предметов, решения о по­грузке которых приняты на этапах i, i + 1,п. Это определение отражает тот факт, что ограничение по весу является единственным, которое связывает п этапов вместе.

Пусть f,(x)— максимальная суммарная прибыль от этапов /', /'+ 1, я при за­данном состоянии Xj. Проще всего рекуррентное уравнение определяется с помо­щью следующей двухшаговой процедуры.

Глава 10. Детерминированные модели динамического программирования

Выразим/;(*,) как функцию,/^,(х_/+1) в виде

/.(*,.)= max {пт,+/_м(х_м)}, / = 1,2,..., я,

г, =0.1.....VV '

где/^х^,) = 0.

Выразим х^, как функцию х,- для гарантии того, что левая часть по­следнего уравнения является функцией лишь X;. По определению х_; - x_Ul представляет собой вес, загруженный на этапе /, т.е. х_г ⁼ WjiTij или X,,, = х_;- иуя_;. Следовательно, рекуррентное уравнение приобретает следующий вид.

/(*,.)= max ^{r_ifn.+f_M(x_i-w_im_i)}, / = 1,2,..., п.

wi,=0.1.....

г, =0.1.....w'

Пример 10.3.1

В 4-тонный самолет загружаются предметы трех наименований. Приведенная ни­же таблица содержит данные о весе одного предмета w, (в тоннах) и прибыли г, (в тысячах долларов), получаемой от одного загруженного предмета. Как необхо­димо загрузить самолет, чтобы получить максимальную прибыль?

Предмет /'	IV;	г.

Так как вес одного предмета w, для всех наименований и максимальный вес W при­нимают целочисленные значения, состояние х, может принимать лишь целочис­ленные значения.

Этап 3. Точный вес, который может быть загружен на этапе 3 (предмет наименования 3), заранее неизвестен, но он должен принимать одно из значений 0, 1, 4 (так как W = 4 тонны). Состояния х₃= 0 и х₃= 4 представляют собой крайние случаи, когда пред­меты третьего наименования совсем не загружаются или загружают самолет полно­стью. Остальные значения х₃ (= 1, 2 или 3) предполагают частичную загрузку самолета предметами третьего наименования. Действительно при этих значениях х₃ все остав­шиеся емкости самолета могут быть заполнены предметами третьего наименования.

Так как вес w₃ одного предмета третьего типа равен 1 тонне, максимальное количе­ство единиц этого типа, которое может быть загружено, равно [4/1] = 4. Это означа­ет, что возможными значениями х₃ будут 0, 1, 2, 3 и 4. Решение т₃ является допус­тимым лишь при условии, что w₃m₃<x₃. Следовательно, все недопустимые альтернативы (те, для которых w₃m₃> х₃) исключены. Следующее уравнение явля­ется основой для сравнения альтернатив на этапе 3.

/₃(х₃) = max{l4m₃}, max{m₃} =

Шаг1.

Шаг 2.

10.3. Приложения динамического программирования 449 В следующей таблице сравниваются допустимые решения для каждого значения х₃.

Xi	14/Пз					Оптимальное решение
т3 = 0	т3 = 1	т3 = 2	т3 = 3	т3 = 4		"h
		—	—	—	—
			—	—	—
				—	—
					—

Этап 2.

/₂(х,) = max{47m, + /₃(x, -3m,)}, тах{/и,} =

= 1.

47/772 + h(x₂ - Зпь) Оптимальное решение

Xl /772 = 0 пь = 1 fi(x₂) _т

0 0+0=0 — 0 0

1 0 + 14=14 — 14 0

2 0 + 28 = 28 — 28 0

3 0 + 42 = 42 47 + 0 = 47 47 1

4 0 + 56 = 56 47+ 14 = 61 61 1

Этап 1.

		/,(*,) = max {3 lm, +/,(*,- Ъщ)}, in,	max{m,} =	'a' _2_	= 2.
Х\	31 т, + f2(xx	-2m,)	Оптимальное решение
mi =0	m, = 1 mi = 2	м(х,)			m\
	0 + 0 = 0	— —
	0 + 14=14	— —
	0 + 28 = 28	31+0 = 31 —
	0 + 47 = 47	31+14 = 45 —
	0 + 61 =61	31 + 28 = 59 62 + 0 = 62

Оптимальное решение определяется теперь следующим образом. Из условия W= 4 следует, что первый этап решения задачи при х_г = 4 дает оптимальное решение ml = 2, которое означает, что два предмета первого наименования будут загружены

в самолет. Эта загрузка оставляет х₂ = x_t - 2 т\ =4-2x2 = 0. Решение на втором этапе при х_г=0 приводит к оптимальному решению т\ =0, которое, в свою оче­редь, дает х₃ = х₂- 3т' = 0-3x0 = 0. Далее этап 3 при х₃ = 0 приводит к т\ =0.

Глава 10. Детерминированные модели динамического программирования

Следовательно, оптимальным решением задачи является т\ =2, т\ = О и т\ = 0* Соответствующая прибыль равна 62 ООО долларов.

В таблице для первого этапа нам, по существу, необходимо получить оптимальное решение лишь для x_t = 4, так как это последний этап, подлежащий рассмотрению. Однако в таблицу включены также вычисления для х, = 0, 1, 2 и 3, которые позво" ляют провести анализ чувствительности решения. Например, что произойдет, если максимальная грузоподъемность самолета будет 3 тонны вместо 4? Новое опти­мальное решение может быть определено, начиная с х, = 3 на первом этапе и про­должая так, как мы поступали при я, = 4.

Задача о загрузке является типичным представителем задачи распределения ресурсов, в которой ограниченный ресурс распределяется между конечным чис­лом видов (экономической) деятельности. При этом целью является максимиза­ция соответствующей функции прибыли. В таких моделях определение состоя­ния на каждом этапе будет аналогично приведенному для задачи о загрузке: состоянием на этапе i является суммарное количество ресурса, распределяемого на этапах i,l+l,п.

Решение задачи о загрузке в Excel. Природа вычислений в динамическом про­граммировании такова, что делает невозможным разработку универсальных про­грамм для решения задач ДП. Возможно, этим объясняется отсутствие на сего­дняшний день коммерческих программных продуктов, рассчитанных на решение широкого класса задач ДП.

Здесь мы покажем, как решается в Excel один подкласс задач ДП — задача о загруз­ке с одним ограничением (файл chlOKnapsack.xls¹). На рис. 10.4 показан рабочий лист Excel для решения задачи о загрузке методом обратной прогонки. Рабочий лист разбит на два раздела. В разделе, ограниченном столбцами Q:V, выводятся результаты вычис­лений. В другом разделе (столбцы А:Р) в его верхней части (строки 3-6) содержатся входные данные для текущего этапа, нижняя часть (строка 7 и ниже) зарезервирова­на для вывода результатов вычислений по этапам. Отметим, что максимальное воз­можное число альтернатив т, на этапе i не должно превышать 10 (ячейки D6:N6).

А

e | с

D

e

F -

о

H

•>

к

L

U

N

О |P

Q - R | S

T, U | V

Dynamic Prog

lammir

q (Backward) Knapsack Model

Input Data and Step* Calculation*

Ouput Solution Summary

Ilumber of *taae*1№*

Re*, limit, W-

••Maximum WAv cannot exceed 10

x 1 m

x 1 m

uirent stage- 1

Are m vatubt correct?

1 Stage

Optimum

r"m«

Solution

в

f m

1

Puc. 10.4. Шаблон Excel для решения задачи о загрузке