Сложность алгоритмов

Применение математики во многих приложениях, требует как правило, использования различных алгоритмов. Для решения многих задач не трудно придумать комбинаторные алгоритмы, сводящиеся к полному перебору вариантов. Но здесь вступает в силу различие между математикой и информатикой: в информатике недостаточно высказать утверждение о существовании некоторого объекта в теории и даже недостаточно найти конструктивное доказательство этого факта, т.е. алгоритм. Мы должны учитывать ограничения, навязываемые нам миром, в котором мы живем: необходимо, чтобы решение можно было вычислить, используя объем памяти и время, приемлемые для человека и компьютера.

Основные понятия

Класс однородных вычислительных задач мы будем называть проблемой ( также используется понятие массовая задача). Индивидуальные случаи проблемы T мы будем называть частными случаями проблемы T. Таким образом, T есть множество всех своих частных случаев. Такое описание проблемы есть только предмет соглашения и удобство обозначений. Мы можем, например, говорить о проблеме умножения матриц. Частные случаи этой проблемы суть (для любого целого n -размера квадратных матриц) пары матриц, которые нужно перемножить.

В качестве другого примера рассмотрим классическую задачу о коммивояжере. Параметры этой массовой задачи состоят из конечного набора "городов" C = {c₁, c₂,..., c_m} и "расстояний" d(c_i, c_j) между каждой парой городов c_i, c_j из C. Решение - это такой упорядоченный набор <c_k(1), c_k(2),..., c_k(m)> заданных городов, который минимизирует величину

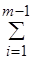d(c_k(i), c_k(i+1)) +d(c_k(m), c_k(1)).

Это выражение дает длину маршрута, начинающегося в городе c_k(1), проходящего последовательно через все города и возвращающегося в c_k(1) непосредственно из последнего города c_k(m). Индивидуальная задача о коммивояжере задается любыми конкретными множествами {c₁, c₂,..., c_m} и {d(c_i, c_j)}.

С каждым частным случаем проблемы I ÎT мы связываем размер | I | (обычно целое число). Эта функция | I | не единственна, и ее выбор диктуется теоретическими и практическими соображениями, связанными с тем, с какой точки зрения интересна эта проблема.

Возвратимся к примеру умножения матриц, отметим, что разумной мерой для пары I =(A,B) (n´n)-матриц, которые надо перемножить, является | I |=n. Если мы изучаем объем памяти, требующейся для алгоритма умножения матриц, то подходящей может быть мера | I |=n². В задаче о коммивояжере | I | можно определить как количество данных городов m.

Пусть T - проблема и A - алгоритм, решающий ее. При решении частного случая I ÎT алгоритм A выполняет некоторую последовательность вычислений S_I. С S_I мы связываем некоторые числовые характеристики.

Существенными являются, например, следующие характеристики:

· длина S_I, которая характеризует время вычисления;

· глубина S_I, т. е. число уровней параллельных шагов, на которые S_I может быть разложено; она соответствует времени, которое S_I потребовалось бы при параллельных вычислениях;

· объем памяти, требуемый для вычисления S_I;

· вместо общего числа шагов в S_I мы можем подсчитывать число шагов некоторого вида, таких как арифметические операции при алгебраических вычислениях, число сравнений при сортировке или число обращений к памяти.

Для аппаратной реализации алгоритмов мы обычно определяем размер | I |, так, чтобы все частные случаи I одинакового размера n решались при помощи одной и той же схемы C_n. Сложность схемы C определяется разными способами, например, как число элементов, глубина, снова связанная со временем вычислений, или выбираются другие меры сложности, такие как число модулей, связанное с технологией, используемой при построении схемы.

После того как выбрана мера m вычисления S функция F_A сложности вычисления может быть определена несколькими способами, два главных из них - сложность в наихудшем случае и сложность поведения в среднем.

Первое понятие определяется следующим образом:

F_A(n) = max {m(S_I) | I ÎT, | I | = n}.

Для того чтобы определить поведение в среднем, мы задаем распределение вероятностей T на каждом множестве T_n = { I | I ÎT, | I | = n}. Так, для I ÎT, | I | = n, величины p (I) - вероятность появления I среди всех других частных случаев размера n. Поведение в среднем алгоритма A тогда определяется так:

M_A(n) =

Анализ алгоритмов связан со следующим вопросом. Для заданной функции размера | I| и меры вычисления m(S_I) точно определить для данного алгоритма A, решающего проблему T, либо сложность F_A для наихудшего случая, либо, при подходящих предположениях, поведение в среднем M_A. Вопросы анализа алгоритмов подробно рассматриваются в трехтомнике Д. Кнута "Искусство программирования для ЭВМ" [15].

Сложность задачи - это сложность наилучшего алгоритма, известного для ее решения.

Для оценок сложности потребуется следующее определение. Будем говорить, что функция f(n) есть O(g(n)), если существует константа C такая, что |f(n)| £ C (g(n)) для всех натуральных n.

Основной вопрос теории сложности: насколько успешно или с какой стоимостью может быть решена заданная проблема T? Мы не имеем в виду никакого конкретного алгоритма решения T. Наша цель - рассмотреть все возможные алгоритмы решения T и попытаться сформулировать утверждение о вычислительной сложности, внутренне присущей T. В то время как всякий алгоритм A для T дает верхнюю оценку величины F_A сложности T, нас интересует нижняя оценка. Знание нижней оценки представляет интерес математический и кроме того, руководит нами в поиске хороших алгоритмов, указывая, какие попытки заведомо будут безуспешны.

Классификация задач по степени сложности

Быстрыми являются линейные алгоритмы, которые обладают сложностью порядка n и называются также алгоритмами порядка O(n), где n - размерность входных данных. К линейным алгоритмам относится школьный алгоритм нахождения суммы десятичных чисел, состоящих из n₁ и n₂ цифр. Сложность этого алгоритма - O(n₁ + n₂). Есть алгоритмы, которые быстрее линейных, например, алгоритм двоичного поиска в линейном упорядоченном массиве имеет сложность O(log₂n), n - длина массива.

Другие хорошо известные алгоритмы - деление, извлечение квадратного корня, решение систем линейных уравнений и др. - попадают в более общий класс полиномиальных алгоритмов.

Полиномиальным алгоритмом (или алгоритмом полиномиальной временной сложности, или алгоритмом принадлежащим классу P) называется алгоритм, у которого временная сложность равна O(n^k), где k - целое число > 0. Алгоритмы, для временной сложности которых не существует такой оценки, называются экспоненциальными.

Задача считается труднорешаемой, если для него не существует разрешающего полиномиального алгоритма.

Заметим, что при небольших значениях n экспоненциальный алгоритм может быть более быстрым, чем полиномиальный (почему?). Однако различие между этими двумя типами задач велико и всегда проявляется при больших значениях n.

Класс P

Мы называем задачу "хорошей" если для нее существует полиномиальный алгоритм. Приведем список некоторых хорошо решаемых задач.

· Рассортировать множество из n чисел. Сложность поведения в среднем порядка O(n log n) для быстрого алгоритма Хоара [26, стр.316-321].

· Найти эйлеровый цикл на графе из m ребер. В силу теоремы Эйлера мы имеем необходимое и достаточное условие для существования эйлерова цикла и проверка этого условия есть алгоритм порядка O(m) [24, стр. 200-201].

· Задача Прима-Краскала. Дана плоская страна и в ней n городов. Нужно соединить все города телефонной связью так, чтобы общая длина телефонных линий была минимальной. В терминах теории графов задача Прима-Краскала выглядит следующим образом: Дан граф с n вершинами; длины ребер заданы матрицей (d[i,j]), i,j = 1,...,n. Найти остовное дерево минимальной длины. Эта задача решается с помощью жадного алгоритма сложности O(n log n)[26, стр.357-358].

· Кратчайший путь на графе, состоящем из n вершин и m ребер. Сложность алгоритма O(m n) [26, стр.377-382].

· Связные компоненты графа. Определяются подмножества вершин в графе (связные компоненты), такие, что две вершины, принадлежащие одной и той же компоненте, всегда связаны цепочкой дуг. Если n - количество вершин, а m - количество ребер, то сложность алгоритма O(n+m) [26, стр.364-365].

· Быстрое преобразование Фурье [6, стр. 284-302], требующее O(n log n) арифметических операций, - один из наиболее часто используемых алгоритмов в научных вычислениях.

· Умножение целых чисел. Алгоритм Шёнхаге-Штрассена [6, стр. 304-308]. Сложность алгоритма порядка O(n log n log log n). Отметим, что школьный метод для умножения двух n-разрядных чисел имеет сложность порядка O(n²).

· Умножение матриц. Алгоритм Штрассена [6, стр. 259-261] имеет сложность порядка O(n^{log 7}), для умножения двух матриц размера n´n. Очевидный алгоритм имеет порядок сложности O(n³).