Пример гидравлического расчета трубопровода

Рассмотрим трубопровод, приведенный на рис. 1.8.

Рассчитаем потери давления на участке 1—2. Исходные данные для расчета:

внутренний диаметр d_1-2=0,05 м=50 мм;

расход Q_1-2=12 м³/ч=0,003 м³/с.

Рис. 1.8. Расчетная схема разветвленного трубопровода.

1, 2, 3, 4, 5 — узловые точки трубопровода.

Решение:

1. По номограмме (см. рис. 1 приложения) определяем скорость жидкости на данном участке

м/с.

2. По известным d, Q и 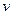по номограмме (см. рис. 1 приложения) находим число Рейнольдса, принимая коэффициент м²/с при °С

.

3. Определяем гидравлический уклон по номограмме (см. рис. 2 приложения), считая трубы участка технически гладкими,

Па/м.

4. Находим единичную эквивалентную длину но номограмме (см. рис. 3 приложения), м.

5. Подсчитываем сумму коэффициентов местных сопротивлений на участке 1—2

,

где — коэффициент сопротивления фильтра;

—коэффициент сопротивления невозвратно-запорного клапана;

— коэффициент сопротивления колена;

—коэффициент сопротивления ответвления;

—коэффициент сопротивления запорного клапана.

6. Вычисляем полную эквивалентную длину участка 1—2

м.

7. Приведенная длина участка 1—2

м.

8. Потери давления на преодоление гидравлических сопротивлений на участке 1—2

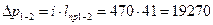Па.

9. Узловое давление p_узл принимаем с запасом относительно полученных расчетом потерь давления на участке 1—2

Па.

Данные расчета участков 2—3 и 3—4 приведены в табл. 1.1.

Потери давления на преодоление гидравлических сопротивлений на участке 1—4 с учетом геометрической высоты всасывания z не должны превышать давления всасывания, создаваемого принятым насосом, т. е. . В нашем случае насос имеет Па, а Па и, следовательно, удовлетворяет этому требованию. Таким образом, на основании расчета можно сделать заключение, что принятые диаметры трубопроводов, вполне допустимы и при необходимости могут быть даже уменьшены.