Проверочный расчет платформы на горизонтальные нагрузки

Горизонтальные нагрузки появляются при повороте в неуста­новившемся режиме, который имеет место в экскаваторах и кра­нах во время разгона и торможения платформы. На платформу и установленные на ней механизмы, силовую установку и рабочее оборудование в это время действуют инерционные нагрузки.

За расчетное положение для экскаватора с оборудованием лопаты принимается положение груженого ковша на максимальном вылете при горизонтальной рукояти; с оборудованием драглайна и крана — поворот с груже­ным ковшом (грузом) на мак­симальном вылете.

При определении инерци­онных нагрузок каждый эле­мент поворотной части можно рассматривать как звено с массой т, центр масс кото­рого не совпадает с его осью вращения.

Инерционные нагрузки при торможении поворотной платформы вызывают в углах платфор­мы, а также в местах уста­новки цапфы, поворотных стаканов и пят стрелы значительные знакопеременные напряжения. Так, при испытаниях платформы экскаватора ЭКХ-6 напряжения при повороте в районе установки пят стрелы и центральной цапфы достигали ±2000 кгс/см² [32]. Точки приложения инерционных нагрузок (обычно их относят к центрам тяжести узлов) в большинстве случаев не совпадают с плоскостью поворотной платформы, а лежат значительно выше ее (рисунок 2.31). В связи с этим можно считать, что платформа работает на изгибающие и сжимающие нагрузки в ее плоскости и на кру­тящий момент М_кр, вызывающий кручение относительно ее продольной оси.

Рисунок 14.31 - Схема инерционных нагрузок при торможении поворотной платформы

Рассмотрим расчет платформы при первом случае нагружения.

На рисунок 14.32, а приведена расчетная схема применительно к плат­форме экскаватора или крана малой мощности на нагрузки, дей­ствующие в ее плоскости.

Для простоты на схеме указаны только составляющие от инер­ционных нагрузок, действующих на рабочее оборудование и на противовес. Поскольку сила инерции в рабочем оборудовании действует на значительном расстоянии от платформы, ее заменяют составляющими P_4и, приложенными к проушинам стрелы, парал­лельным ей, и R_4и, образующими момент, равный по величине и направлению моменту от силы инерции относительно пят стрелы. Такое упрощение является допустимым для расчета боль­шинства платформ на инерционные нагрузки, так как инерционные нагрузки от механизмов и надстроек сравнительно малы.

Положение опор в приведенной расчетной схеме соответствует одному из вариантов размещения центральной цапфы и стаканов поворотных механизмов. Опорные реакции в центральной цапфе R_ц и поворотном стакане R_n находят из равенства мо­ментов инерционных и ре­активных сил.

Как видно из рисунка, расчет платформы на рас­сматриваемые нагрузки в этом случае может быть сведен к расчету рамы на нагрузки в ее плоскости. Для расчета такой рамы целесообразно применить метод сил. Учитывая сим­метрию расчетной схемы относительно продольной оси и несимметричность внешней нагрузки, в данном случае представляется возможным значительно упростить канонические уравнения. Этому удовлетворяет основная система, приведенная на рисунке 14.32, б.

Рисунок 14.32 - Схемы к расчету платформы на горизонтальные нагрузки при повороте

Как видно, в данном случае система трижды статически не­определима. Канонические уравнения для нее имеют обычный вид. Эпюры и для нахождения коэффициентов и приведены на рисунок 2.33.

Рисунок 14.33. Схемы к расчету поворотной платформы на горизонталь­ные нагрузки

На практике выходной вал поворотного механизма часто размещается и в передней части платформы. Расчетная схема в этом случае аналогична схеме, приведенной на рисунке 14.34.

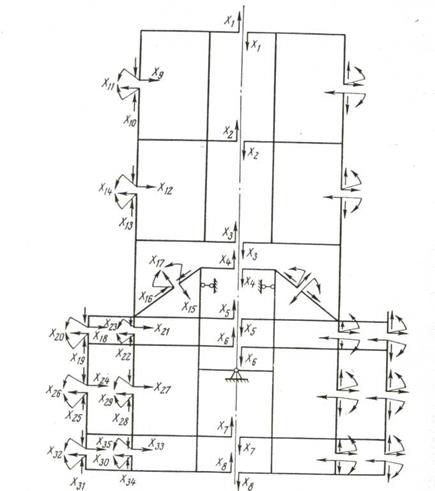
Рисунок 14.34 - Основная система для расчета платформы шагающего экскаватора на горизонтальные нагрузки

Встречаются конструкции и со смещенным относительно про­дольной оси платформы стаканом. Тогда в основной системе для этого варианта в соответствующем сечении поперечной балки принимают три неизвестных, что увеличивает число канонических уравнений на два.

В экскаваторах средней и большой мощности, где число продольных балок обычно более четырех, количество неизвестных канонических уравнений при расчете на горизонтальные нагрузки значительно увеличивается. Так, при расчете платформы, представленной на рисунок 14.34, в, число неизвестных достигает 35. Это бывает, если за основную систему принята система, приведенная на рисунок 14.34.

Как видно из рисунка, несмотря на значительное усложнение основной системы, она в то же время имеет и много общего с си­стемой, приведенной на рисунок 14.34, для малых машин.