Проверочный расчет поворотной платформы на вертикальные нагрузки. Проверочный расчет поворотной платформы на горизонтальные нагрузки

Расчетные схемы платформ, представленные на рисунке 14.27, с уче­том симметрии относительно продольной оси могут быть приве­дены к видам, изображенным на рисунок 14.29 и 14.2. При этом расчет­ная схема, изображенная на рисунке 14.29, соответствует расчетной схеме поворотных платформ, в которых опрокидывающий момент воспринимает центральная цапфа (опора В). Схема, представлен­ная на рисунке, соответствует расчетной схеме поворотных плат­форм, в которых опрокидывающий момент воспринимается кат­ками-захватами или хвостовыми роликами (шариками) опорного круга. Так как в роликовых и шариковых кругах зазор между роликами (шариками) и опорными кольцами при опрокидывании незначителен, опору С в этом случае размещаем на пересечении хвостовой части опорного круга с продольной балкой. Там, где продольные балки разнесены на величину, равную или близкую диаметру роликового (шарикового) круга, за расчетную следует принимать схему, изображенную на рисунке. Только опору В в этом случае следует перенести на место пересечения балки Б1 с продольной балкой.

Приведенные на рисунок 14.29 и 14.30 схемы представляют собой один раз статически неопределимые системы. За неизвестное в основной системе (рисунок 2.29) примем реакцию в опоре В, а в системе (рисунок 14.30) — реакцию в опоре С. Канонические уравнения имеют следующий вид:

Рисунок 14.29 - Схемы к расчету продольной и поперечной балок платформы при работе центральной цапфы

Рисунок 14.30 -. Схемы к расчету продольной и поперечной балок платформы при катках-захватах или роликовом круге

при восприятии опрокидывающего момента центральной цап­фой

(14.115)

при восприятии опрокидывающего момента катками-захватами

; (14.116)

при восприятии опрокидывающего момента роликами (шари­ками) опорного круга

. (14.117)

Коэффициенты канонических уравнений и определяют по формуле Мора на основании эпюр изгибающих момен­тов и .

Величина k₁ в уравнении (2.115) представляет собой коэффи­циент упругой податливости опоры В,который численно равен прогибу конца поперечной балки Б2 от единичной нагрузки, при­ложенной в середине ее пролета:

.

После определения неизвестных Х₁ опорные реакции R_A и R_Б вточках А и Б легко могут быть найдены из основных систем, представленных на рисунок 2.29 и 17.2. Так, для схемы по рисунку 2.29

, (14.118)

а для схемы по рисунку 2.30

, (14.119)

Полная реакция R_D передней поперечной балки с учетом двух половин платформы

R_D = 2R_a.

Реакция R_Б найдется из суммы проекций всех сил, действую­щих на продольную балку, на вертикальную ось.

По найденным нагрузкам строится результирующая эпюра из­гибающих моментов . Зная изгибающий момент в исследуе­мом сечении балок платформы и их геометрические параметры, можно найти напряжения от вертикальных нагрузок в этих се­чениях.

Нормальные напряжения в точках сечений балок вблизи их взаимного пересечения следует определять с учетом стесненного изгиба по формуле

, (14.120)

где k — коэффициент учета дополнительных напряжений от стес­ненного изгиба.

Касательные напряжения от поперечных сил Q определяют по формуле

балках двутаврового сечения

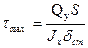, (14.121)

где S — статический момент сопротивления половины сечения от­носительно нейтральной оси балки х — х.