 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
ПРЕДЕЛЫ. Число а называется пределом последовательности если для всякого сколь угодно малого положительного числа ε найдётся такое положительное число N
|
|
Число а называется пределом последовательности 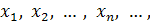 если для всякого сколь угодно малого положительного числа ε найдётся такое положительное число N, что
если для всякого сколь угодно малого положительного числа ε найдётся такое положительное число N, что 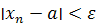 при n > N.
при n > N.
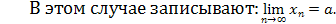
Число A называется пределом функции f(x) при x → a, если для любого сколь угодно малого ε > 0 найдётся такое δ > 0, что ׀ f(x) – A׀ < ε при
 .
.
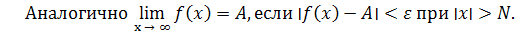
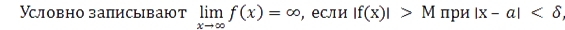
где M – произвольное положительное число.
В этом случае функция f(x) называется бесконечно большой величиной при x → a.
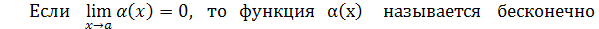
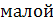 величиной при x → a.
величиной при x → a.
Если x < a и x → a, то условно пишут x → a – 0; если x > a и x → a, то пишут x → a + 0.
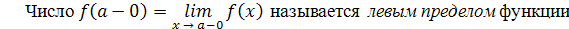
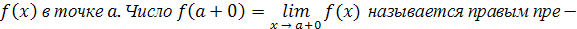
делом функции f (x) в точке a.
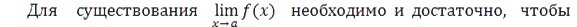
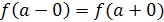
Практическое вычисление пределов основывается на следующих теоремах.

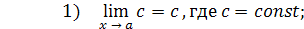
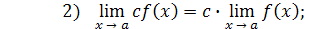
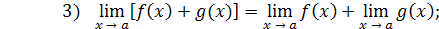
4) 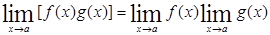
5) 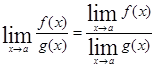 при (
при (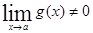 )
)
Используются также первый и второй замечательные пределы:
1) 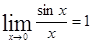
2) 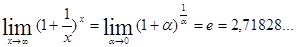
Логарифм числа x по основанию e называется натуральным логарифмом и обозначается ln x.
При решении примеров полезно иметь в виду следующие равенства:
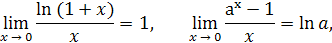

Пример 9. Показать, что при n →∞ последовательность 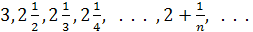 имеет пределом число 2.
имеет пределом число 2.
Решение. Здесь n –й член последовательности 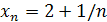 . Следовательно,
. Следовательно, 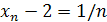 . Зададим заранее положительное число ε. Выберем n настолько большим, что будет выполняться неравенство 1/ n < ε. Для этого достаточно принять n > 1/ε. При таком выборе n будем иметь
. Зададим заранее положительное число ε. Выберем n настолько большим, что будет выполняться неравенство 1/ n < ε. Для этого достаточно принять n > 1/ε. При таком выборе n будем иметь  . Следовательно,
. Следовательно, 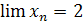 .
.
Пример 10. Показать, что при n → ∞ последовательность 7/3, 10/5,
13/7,..., (3n + 4) /(2n + 1),... имеет пределом число 3/2.
Решение. Здесь  3/2 = (3n + 4) /(2n + 1) – 3/2 = 5/
3/2 = (3n + 4) /(2n + 1) – 3/2 = 5/ 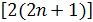 . Определим, при каком значении n выполняется неравенство
. Определим, при каком значении n выполняется неравенство
5/ 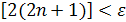 ; так как 2(2n + 1) > 5/ε, то n > 5/4ε – 1/2.
; так как 2(2n + 1) > 5/ε, то n > 5/4ε – 1/2. 
Положив ε = 0,1, заключаем, что неравенство 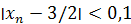 выполняется при n > 12 (например, при n = 13).
выполняется при n > 12 (например, при n = 13).
Неравенство 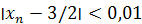 выполняется при n > 124,5 (например, при n = 125).
выполняется при n > 124,5 (например, при n = 125).
Неравенство  выполняется при n > 1249,5 (например, при n = 1250).
выполняется при n > 1249,5 (например, при n = 1250).
Пример 11.

Решение. Так как x → 4, то числитель дроби стремится к числу
5 · 4 + 2 = 22, а знаменатель к числу 2 · 4 + 3 = 11.
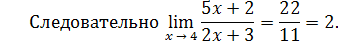
Пример 12.
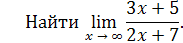
Решение. Числитель и знаменатель дроби безгранично возрастают при
x → ∞. В таком случае говорят, что здесь имеет место неопределённость вида  .
.
Разделив на x числитель и знаменатель дроби, получаем
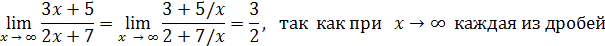

Пример 13.
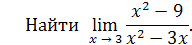
Решение. Здесь числитель и знаменатель дроби стремятся к нулю при
x → 3 (принято говорить, что получается неопределённость вида 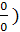 .
.

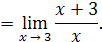
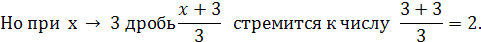
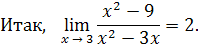
Пример 14.
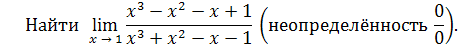
Решение. Разложим на множители числитель и знаменатель дроби:
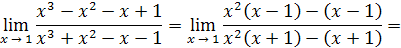
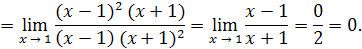
Пример 15.
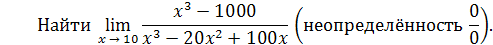
Решение. Имеем
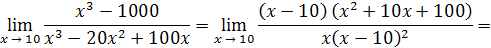
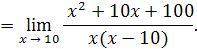
Числитель дроби стремится к 300, а знаменатель стремится к нулю, т.е. является бесконечно малой величиной, следовательно, рассматриваемая дробь –бесконечно большая величина и

Пример 16.

Решение. Умножим числитель и знаменатель дроби на сумму
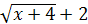 :
:
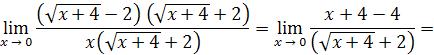
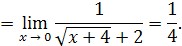
Пример 17.
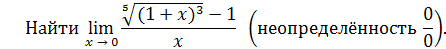
Решение. Положим  , тогда
, тогда
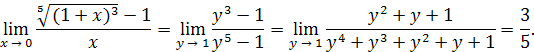
Пример 18.
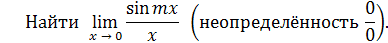
Решение. Имеем
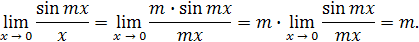
Пример 19.
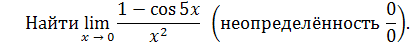
Решение. Имеем
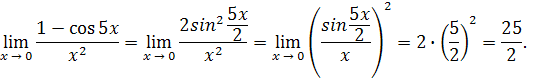
Здесь мы воспользовались результатом предыдущего примера, приняв
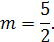
Пример 20.
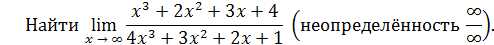
Решение. Разделим числитель и знаменатель дроби на старшую степень x, т.е. на 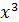 :
:
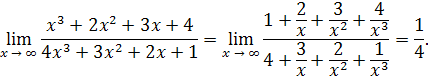
Пример 21.

Решение. Разделим числитель и знаменатель на 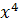 :
:
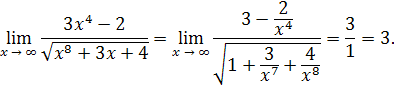
Пример 22.

Решение. Умножим и разделим рассматриваемое выражение на
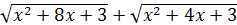 :
:
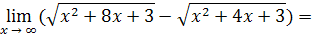
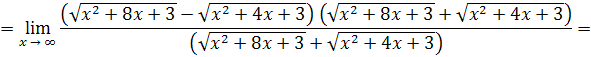
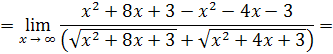
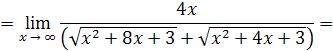
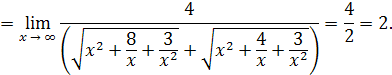
Пример 23.
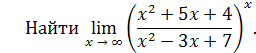
Решение. Делением числителя дроби на знаменатель выделим целую часть:

Таким образом,
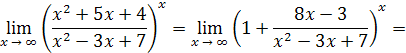
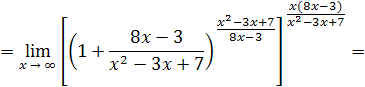
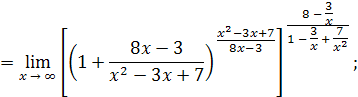
так как
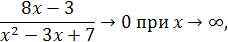
то
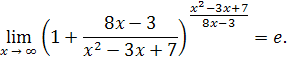
Приняв во внимание, что
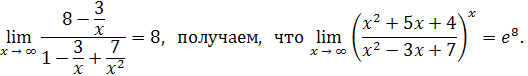
Пример 24. Найти левый и правый пределы функции

при x → 3.
Решение.
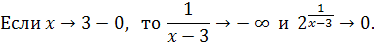
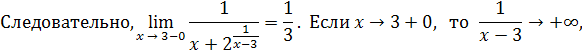
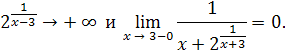
Пример 25. Найти левый и правый пределы функции 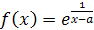 при
при
x → a.
Решение.
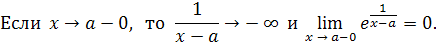
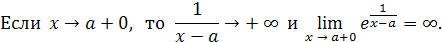
Дата публикования: 2014-11-18; Прочитано: 832 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
