Построение графиков функций

При построении графиков функций применяются следующие приёмы:

а) построение «по точкам»;

б) действия с графиками (сложение, вычитание, умножение графиков);

в) преобразования графиков (сдвиг, растяжение).

Исходя из графика функции y = f(x), можно построить графики функций:

1) y = f (x – a) – первоначальный график, сдвинутый вдоль оси Оx на величину a;

2) y = f (x) + b – тот же график, сдвинутый вдоль оси Oy на величину b;

3) y = A · f (x) – исходный график, растянутый в A раз вдоль оси Oy;

4) y = f (kx) – тот же график, сжатый в k раз вдоль оси Ox.

Таким образом, можно по графику функции y = f (x) построить график функции вида .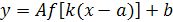

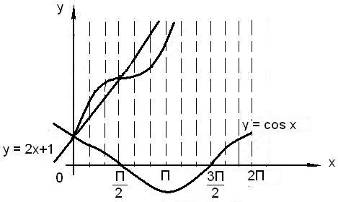
Рис. 1

Пример 6. Построить график функции y = 2 x + 1 + cos x.

Решение. График данной функции можно построить путём сложения графиков двух функций: y = 2 x + 1, y = cos x. График первой функции есть прямая, её можно построить по двум точкам, график второй функции–косинусоида(Рис. 1).

Пример 7. Построить график функции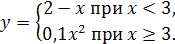

Решение. При x < 3 графиком является луч прямой, а при x ≥ 3 – ветвь параболы. Искомый график изображен на рис. 2.

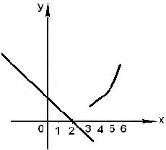
Рис. 2

Пример 8. Построить график функции y = 2 sin (2 x – 1) или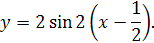

Решение. Здесь Исходный график y = sin x. Затем строим график функции y = sin 2x путём сжатия вдоль оси абсцисс в два раза. После этого строим график функции 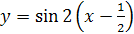путём сдвига 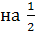вправо и, наконец, искомый график функции y = 2 sin (2 x – 1) путём растяжения вдоль оси ординат графика (3) в два раза (рис. 3).

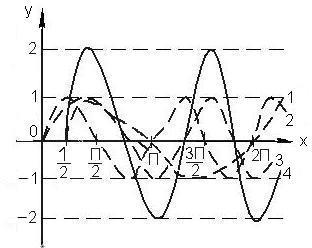
Рис.3