Основні закони Булевої алгебри: аксіоми математичної логіки

1. Комутативність диз’юнкції і кон’юнкції*. Слово комутативний означає – переміщувальний (переместительный). Цей закон, який виражає незалежність суми або добутку від перестановки доданків (слагаемых) або множників.

2. Асоціативність диз’юнкції і кон’юнкції*. Слово асоціативний означає – сполучений (сочетательный). Це закон, який виражає незалежність суми або добутку від заміни деяких доданків їх сумою або деяких множників їхнім добутком.

3. Дистрибутивність кон’юнкції відносно диз’юнкції* і диз’юнкції відносно кон’юнкції. Слово дистрибутивний означає – розподілю вальний (распределительный). Це закон, який виражає незалежність добутку алгебраїчної суми на яке-небудь число від заміни на алгебраїчну суму добутків окремих доданків на це ж число.

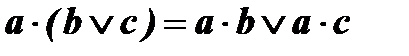
4. Закон ідемпотентність (рівнодія, повторення, тавтологія)*.

5. Закони, що визначають дії з константами *.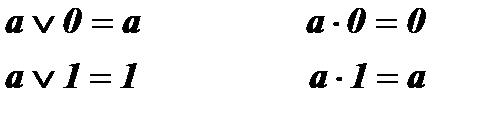

6. Закон виключеного третього *.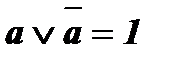

7. Закон протиріччя *

8. Закон подвійного заперечення *.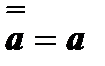

9. Закон де Моргана *.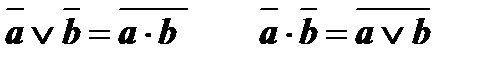

10. Закон поглинання *.

11. Закон склеювання *.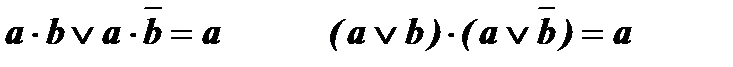

12. Закон Парецького *

Обчислення значень логічних виразів полягає у заміні булевих змінних у виразі їх значеннями і виконанні з цими значеннями передбачених виразом операцій*.

Послідовність виконання операцій:

1) вирази у дужках;

2) вирази під знаком заперечення (інверсії);

3) кон’юнкції;

4) диз’юнкції.

Приклад: хай булеві змінні мають такі значення:

a = 1; b = 0; c = 1; d = 0.

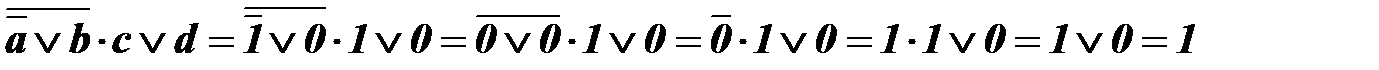Тоді:

Тотожні перетворення логічних виразів полягають у застосуванні до їх частин або виразів в цілому основних законів булевої алгебри.

Метою таких перетворень є зменшення витрат на обчислення значень логічних виразів та їх аналіз за рахунок спрощення цих виразів.

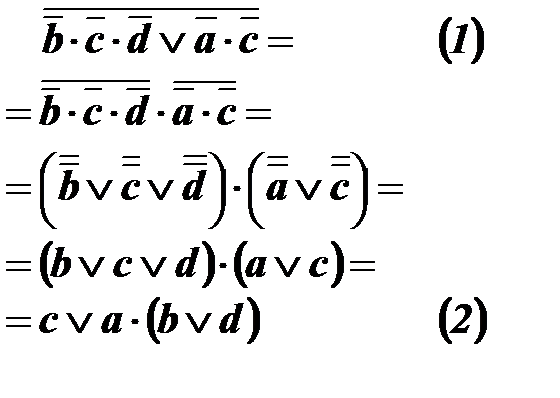Приклад:

Вираз (1)* потребує для обчислення виконання 10-и операцій.

Вираз (2)* потребує для обчислення виконання 3-х операцій.

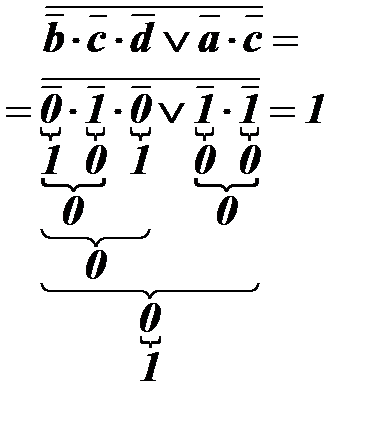
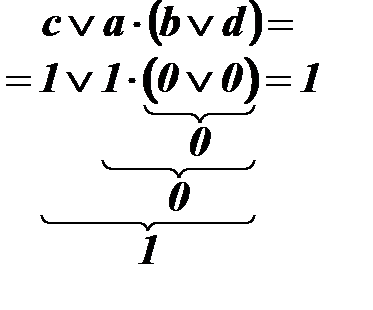
Для багатьох практичних застосувань велике значення мають перетворення та спрощування формул, які побудовані за допомогою булевих функцій. Найпростіший спосіб встановлення еквівалентності формул складається з перевірки збігання стовпців значень відповідних функцій у загальній таблиці їх визначення. Перетворення логічних виразів можна з’ясувати шляхом розглядання інших елементарних функцій, а саме – поетапної побудови їх таблиць істинності.