Теорема Котельникова

Согласно теореме Котельникова, если спектр сигнала ограничен полосой , то сигнал может быть восстановлен по своим отсчётам , разделёнными интервалом времени :

, (1.1)

где .

Предполагается, что число отсчетов бесконечно, (интервал наблюдения - бесконечен).

Ввиду того, спектр сигнала ограничен полосой (вне этой полосы он равен нулю), спектральную функцию сигнала можно представить как периодическую функцию. При увеличении интервала дискретизации больше, чем , спектральные функции сигнала на каждом периоде перекрываются, что приводит к искажению восстановленного сигнала. С уменьшением интервала дискретизации качество восстановленного сигнала улучшается.

Если сигнал ограничен временем наблюдения , то можно осуществить периодическое продолжение его с периодом, равным . В этом случае производится дискретизация спектральной функции с интервалом , и производится восстановление спектральной функции 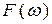по его отсчётам в частотной области:

,

где .

Восстановление спектральной функции будет улучшаться, если интервал дискретизации уменьшать по сравнению с .

Рассмотрим приложение теоремы Котельникова к случайным процессам. Трудность непосредственной записи формулы (1.1) в применении к случайным процессам связано с тем, что имеется множество реализаций, случайного процесса.

Поэтому применяется понятие сходимости в среднеквадратическом [*Левин кн 2 ]

Положим, - непрерывный в среднеквадратическом, стационарный, хотя бы в широком смысле, случайный процесс со спектральной плотностью мощности , .

Если существует предел

,

тогда случайный процесс определяется счётным множеством случайных величин и записывается как

. (1.2)

В качестве критерия возможности представления случайного процесса в виде разложения (1.1) выберем равенство корреляционных функций процесса правой части равенства (1.1). Положим, - корреляционная функция процесса .

Обозначим правую часть (1.1) через . Корреляционная функция процесса равна

=

. *

Сделаем замену

Для произвольной задержки справедливо разложение функции в ряд Котельникова и его представление в виде (Левин Б.Р. Статистические основы радиотехники, книга 2, стр.273)

Применяя это соотношение к , получим

.

Но учитывая, что корреляционная функция – четная функция, имеем

. (1.3)

Но (1.6) - есть разложение корреляционной функции по ортогональным функциям вида т.е.

= .

Исходя из принятого критерия, получим равенство (1.1)