Геометрическая нелинейность

Пример 1. Зависимость периода колебаний математического маятника от амплитуды колебаний по формуле 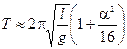– типичное проявление геометрической нелинейности, которая приводит к нелинейности дифференциального уравнения 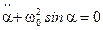колебаний маятника. Эта нелинейность обусловлена зависимостью момента силы тяжести, действующей на маятник, от угла отклонения массы от положения равновесия.

Пример 2. Тело, прижимается к горизонтальной плоскости пружиной. Найдем зависимость проекции F _x(x) силы упругости от перемещения х.

Пусть трение отсутствует и пружина - линейная, т.е. 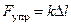, где D l – деформация пружины.

Считаем, что при x =0, F _упр= F ₀, т.е. в положении равновесия пружина натянута. Тогда 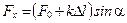, причем .

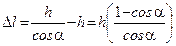Следовательно, 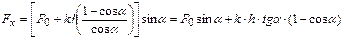. Учитывая, 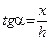, выражая cos a через 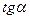, получим .

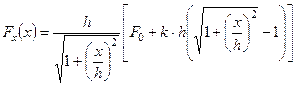Рассмотрим несколько частных случаев (приближений):

Первый случай. Пусть 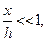тогда, пренебрегая 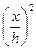, получим

Второй случай (учет слагаемых 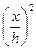). Воспользуемся формуло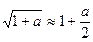й , при 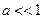. Тогда .

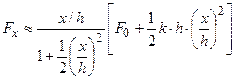Третий случай: начальное натяжение пружины отсутствует, т.е. F ₀=0. Тогда из предыдущей формулы найдем .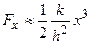

Из полученных формул видно, что результат существенно зависит от используемого приближения, т.е. математической модели. При этом, несмотря на то, что пружина была выбрана линейной, т.е. 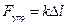, зависимость силы от перемещения может быть существенно нелинейной.