 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Операции с вероятностями
|
|
А чему равна вероятность того, что среди выбранных трех карт есть пиковая дама? Число всех таких исходов нетрудно посчитать, надо просто из всех исходов N вычесть все те исходы, в которых дамы пик нет, т. е. вычесть найденное в примере 4 число N(А). Затем эту разность N – N(А) в соответствии с классической вероятностной схемой следует поделить на N. Вот что получим: 
.
Мы видим, что между вероятностями двух событий имеется определенная связь. Если событие А заключается в отсутствии дамы пик, а событие В состоит в ее наличии среди выбранных трех карт, то
Р(В) = 1 – Р(А);
Р(А) + Р(В) = 1.
К сожалению, в равенстве Р(А) + Р(В) = 1 нет никакой информации о связи событий А и В между собой; эту связь нам приходится держать в уме. Удобнее было бы заранее дать событию В название и обозначение, явно указывающие на его связь с А.
Определение 1. Событие В называют противоположным событию А и обозначают В = 
, если событие В происходит тогда и только тогда, когда не происходит событие А.
Символ можно читать так: «А с чертой». Иллюстрация этого определения приведена на рисунке 5.1.
ТЕОРЕМА 1. Для нахождения вероятности противоположного события следует из единицы вычесть вероятность самого события: Р( ) = 1 - Р(А).
|
Рисунок 5.1
В самом деле, 
На практике вычисляют то, что проще найти: или Р(А), или Р(). После этого пользуются формулой из теоремы и находят, соответственно, или Р(А) = 1 - Р(), или Р() = = 1 - Р(А).
Пример 5. Из колоды в 36 карт случайным образом вытаскивают 5 карт. Какова вероятность того, что среди выбранных карт будет хотя бы одна карта бубновой масти?
Решение. Из множества в 36 элементов мы производим выбор пяти элементов, причем порядок этих элементов не важен. Значит, возможно получение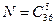 
исходов. Будем действовать по классической вероятностной схеме, т. е. предположим, что все эти исходы равновероятны между собой.
Если А – интересующее нас событие, то противоположное ему событие состоит в том, что среди выбранных пяти карт нет ни одной карты бубновой масти. Но это значит, что все 5 карт выбраны из других карточных мастей, т. е. из 36 - 9 = 27 карт. Значит, N(А) = 
и можно легко найти вероятность события А: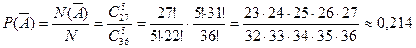 
.
Теперь по теореме находим вероятность самого события А: Р(А) = 1 - Р() ≈ 0,786.
Как видим, вероятность довольна высока. Кстати, полезное напоминание: без калькулятора вычислить вероятность более или менее сложного события бывает затруднительно.
Ответ: ≈ 0,786.
В теории вероятностей используются различные стандартные игровые ситуации. Это бросание монеты или игрального кубика, вытаскивание карт из колоды. К этому списку добавим еще одну, назовем ее «урновая схема»: в темном ящике (урне) лежат неотличимые на ощупь шары различного цвета. Один или несколько шаров вытаскивают. Вычисляют вероятность того, что выбранные шары имеют какой-то определенный набор цветов.
Пример 6. В урне лежат 10 белых и 11 рыжих шаров. Случайным образом достают 5 шаров. Какова вероятность того, что среди этих 5 шаров ровно 3 белых?
Решение. Шары в урне предполагаем неразличимыми, из 21 шара случайным образом производят выбор 5 шаров, причем порядок выбора не важен. Значит, существует N = 
способов такого выбора. Считаем все эти способы равновероятными.
Интересующее нас событие А наступает, когда 3 из 5 шаров – белые, а 2 – рыжие. Из 10 белых шаров, имеющихся в урне, 3 шара можно выбрать 
способами, а из 11 рыжих шаров 2 шара – 
способами. Выбор разноцветных шаров считаем независимым. По правилу умножения получаем, что нужный нам состав шаров можно выбрать N(А) = • способами. Остается посчитать вероятность.
(почти одна треть).
Ответ: ≈ 0,324.
Часто используется способ решения той или иной задачи «перебором случаев», когда условия задачи разбиваются на взаимоисключающие друг друга случаи, каждый из которых рассматривается отдельно. Например, «направо пойдешь – коня потеряешь, прямо пойдешь – задачу по теории вероятности решать будешь, налево пойдешь –...». Или при построении графика функции у =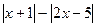 
рассматривают случаи х < -1; 
; 
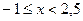. В каждом из трех случаев «раскрывают» модуль, строят нужные графики линейных функций и затем объединяют соответствующие части этих графиков; фактически речь идет о построении графика кусочной функции. Этот же метод часто используют и при подсчете вероятностей.
Пример 7. Из 50 точек 17 закрашены в синий цвет, а 13 – в оранжевый цвет. Найти вероятность того, что случайным образом выбранная точка окажется закрашенной.
Решение. Всего закрашено 30 точек из 50. Значит, вероятность равна 
Ответ: 0,6.
Рассмотрим, однако, этот простой пример более внимательно. Пусть событие А состоит в том, что выбранная точка – синяя, а событие В состоит в том, что выбранная точка – оранжевая (рисунок 5.2). По условию, события А и В не могут произойти одновременно.
 |
Обозначим буквой С интересующее нас событие. Событие С наступает тогда и только тогда, когда происходит хотя бы. одно из событий А или В. Ясно, что N(С) = N(А) + N(В).
Рисунок 5.2
Поделим обе части этого равенства на N – число всех возможных исходов данного опыта; получим 
.
Мы на простом примере разобрали важную и часто встречающуюся ситуацию. Для нее есть специальное название.
Определение 2. События А и В называют несовместными, если они не могут происходить одновременно. В противном случае события называются совместными.
Рисунок 5.3
ТЕОРЕМА 2. Вероятность наступления хотя бы одного из двух несовместных событий равна сумме их вероятностей.
При переводе этой теоремы на математический язык возникает необходимость как-то назвать и обозначить событие, состоящее в наступлении хотя бы одного из двух данных событий А и В. Такое событие называют суммой событий А и В и обозначают А + В.
Если А и В несовместны, то
Р(А + В) = Р(А) + Р(В).
Несовместность событий А и В удобно иллюстрировать следующим рисунком (рисунок 5.4). Если все исходы опыта – некоторое множество точек на рисунке, то события А и В – это некоторые подмножества данного множества. Несовместность А и В означает, что эти два подмножества не пересекаются между собой. Типичный пример несовместных событий – любое событие А и противоположное событие А.
Рисунок 5.4
Разумеется, указанная теорема верна и для трех, и для четырех, и для любого конечного числа попарно несовместных событий. Вероятность суммы любого числа попарно несовместных событий равна сумме вероятностей этих событий.
Рисунок 5.5
Это важное утверждение как раз и соответствует способу решения задач «перебором случаев»:
Пример 8. В урне лежат 10 белых и 11 рыжих шаров. Случайным образом достают 5 шаров. Какова вероятность того, что среди этих шаров есть, по крайней мере, 4 белых шара?
Решение. Всего имеется N = исходов данного испытания. Обозначим буквой С интересующее нас событие. Тогда возможны два случая. Может случиться, что среди 5 выбранных шаров будет ровно 4 белых шара. Обозначим это событие буквой А. А может случиться, что все 5 выбранных шаров – белые, а рыжих нет вовсе. Обозначим это событие буквой В. Тогда А и В – несовместные события, в сумме дающие событие С. Значит, Р(С) = Р(А + В) = Р(А) + Р(В).
Вероятность события А считается так же, как и в примере 6:
.
Так же подсчитывается и вероятность события В.
Значит, Р(С) = Р(А) + Р(В) = 0,114 + 0,012 = 0,126.
Ответ: ≈ 0,126.
Пример 9. В урне лежат 10 белых и 11 рыжих шаров. Случайным образом достают 5 шаров. Какова вероятность того, что среди этих 5 шаров есть, по крайней мере, 3 белых шара?
Решение. Пусть А – событие, состоящее в том, что среди выбранных пяти шаров есть роено 3 белых шара, В – событие, состоящее в том, что белых шаров роено 4, и С – событие, означающее, что все 5 выбранных шаров – белые. Тогда события А, В, С попарно несовместны, а нам требуется найти вероятность того, что произойдет или событие А, или событие В, или событие С. Вероятности каждого из этих событий в отдельности нами уже найдены (примеры 6 и 8). Значит, по теореме 2, Р(А + В + С) = Р(А) + Р(В) + Р(С) = 0,324 + 0,114 +…+ 0,012 = 0,45.
Ответ: = 0,45.
Мы видим, что и между событиями, происходящими в результате некоторого опыта, и между вероятностями этих событий могут быть какие-то соотношения, зависимости, связи и т. п. Например, события можно «складывать», а вероятность суммы несовместных событий равна сумме их вероятностей.
Произведением конечного числа событий называется событие, состоящее в том, что каждое из них произойдет.
Дата публикования: 2014-11-18; Прочитано: 1288 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
