 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Бинарные отношения
|
|
Начнем с примеров. Натуральные числа могут быть полными
квадратами, как 4, 81, 144, или не быть ими, как 5, 30, 48. Это свойство,
или признак числа можно трактовать как принадлежность к
определенному подмножеству натуральных чисел - полных квадратов
{О, 1, 4, 9, 16, 25,...}. То же можно сказать про признак "Х>2" для
действителы-.ых чисел: число 5 обладает этим свойством, а число 1 -
. нет. Напротив, неравенство X > Y выражает свойство не одного числа
•• X или Y, а совокупное свойство пары чисел: если X — 5, Y - 3, то
неравенство выполняется, а для пар (5, 10) и (3, 5) не выполняется.
Можно выразить это так: условие X > Y выполнено для определенного Множества пар чисел.
Некоторые понятия как в математике, так и в обычном языковом ^Потреблении самими своими названиями предполагают отношения
между субъектами или объектами: участник (какого-то мероприятия или коллектива), сосед, знакомый (чей-то), одноименный, сопоставимый (с кем-либо или чем-либо), отличающийся (от чего-то другого), внутри, снаружи, между, обратная функция, обратная теорема. В последнем случае, как мы знаем, если А - обратная теорема (по отношению к теореме В), то и В является обратной к А, так что этот термин характеризует не само утверждение А, а его взаимоотношение с другим утверждением. Также не бывает взаимно-однозначного множества -этим термином обозначается соответствие между двумя множествами.
Пусть задано непустое множество М п -арное (/7-местное) отношение на множестве Л/ - подмножество  ; обозначение
; обозначение
 Говорят, что элементы, составляющие кортеж
Говорят, что элементы, составляющие кортеж
 находятся в отношении R, причем это свойство не
находятся в отношении R, причем это свойство не
отдельных элементов, а именно их совокупности. Полезно рассматривать и одноместное (унарное) отношение - оно называется признаком, или
свойством элементов множества М. В более общем смысле п -арное отношение можно определить и для совокупностей элементов различных
множеств  как подмножество
как подмножество 
Число п называется арностью, или местностью отношения. Чаще других используется случай п = 2.
Бинарное (двуместное) отношение - множество пар
 ; обозначение - R(a,b) или aRb - элементы а и
; обозначение - R(a,b) или aRb - элементы а и
b находятся в отношении R.
Примеры. 1) Отношение равенства между двумя или несколькими числами, фигурами, множествами
2) Бинарное отношение старшинства между людьми по возрасту или воинскому званию.
3) Бинарные родственные и другие отношения между людьми "быть отцом", "быть внуком", "быть одноклассниками".
4) Трехместное (тернарное) отношение "между" для тройки точек
(А,В,С) на прямой: точка А расположена между точками В и С-
5) Тернарное отношение для тройки точек на плоскости - "лежать на одной прямой".
6) Четырехместное отношение для точек пространства -"принадлежать одной плоскости".
7) Четырехместное отношение для чисел - "быть
пропорциональными", т е. удовлетворять соотношению XIY - Z / Т.
8) Бинарное отношение между целыми числами - "иметь
одинаковые остатки от деления на 7"
9) Бинарное отношение {(1, 3), (4, 2), (4, 5), (3, 1), (2, 5), (3, 2)} можно рассматривать просто как 6 пар натуральных чисел (см рис 12); однако этот пример может иметь и содержательный смысл: например, для 5 авторов 1, 2, 3, 4, 5 пара (X, Y) означает, что автор X в своих работах ссылается на автора Y.
Отношение - понятие очень широкое. Так, можно рассматривать отношение принадлежности
элемента а множеству Л/ как 
бинарное отношение между объектами а и М, выполненное для всех пар (а,М) таких, что 
Поскольку п -арные отношения являются множествами, то к ним применимы все теоретико-множественные операции, объединение, пересечение, дополнение и др. Так, объединение отношений " X > Y " и " X = Y " на числовом множестве есть отношениеа
дополнение к последнему есть отношение " X < Y". 
Еще один важный пример - отношение включения для множеств.
Булеан В(Е) - множество всех подмножеств множества Е. Булеан В(Е) обозначается также  . Если М, N - подмножества Е и М есть подмножество множества N, то
. Если М, N - подмножества Е и М есть подмножество множества N, то 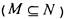 - бинарное отношение
- бинарное отношение
на В(Е).
Равенство отношений  есть равенство множеств
есть равенство множеств  ,
,
определяющих эти отношения, хотя бы они были выражены по-разному Например, отношения между натуральными числами "иметь одинаковые остатки от деления на 2" и "давать при сложении четное число" совпадают. Действительно, остатки от деления двух чисел р и q на 2 равны, если они оба четные (в этом случае остаток - 0) или оба нечетные (остаток 1) То же при сложении чисел р и q: если сумма четная, то оба
слагаемых - одной четности, так как сумма четного и нечетного чисел - нечетна.
Бинарное отношение на конечном множестве можно представить квадратной матрицей, у которой строки и столбцы - это элементы
множества, а элемент матрицы, находящийся на пересечении строки X и столбца У равен 1, если XRY, и равен 0 в противном случае. Пример. Пусть М {а, Ь, с]. Рассмотрим 4 отношения:
V  j
j
Бинарное отношение можно изобразить схемой - см. рис.13, -сопоставив элементам множества точки (вершины), а парам (а,Ь) R  -связки (линии со стрелками, идущие из а в b).
-связки (линии со стрелками, идущие из а в b).
Отношение ARB можно рассматривать и как совокупность всех высказываний вида "элемент  находится в отношении R с
находится в отношении R с
элементом. Поэтому для отношений содержательными являются
определяемые  естественным образом логические операции или связки' дизъюнкция, конъюнкция, отрицание, которые порождают составные отношения; так, например, отрицание бинарного отношения R на множестве М есть бинарное отношение
естественным образом логические операции или связки' дизъюнкция, конъюнкция, отрицание, которые порождают составные отношения; так, например, отрицание бинарного отношения R на множестве М есть бинарное отношение  , в котором
, в котором
находятся все пары элементов из М, кроме находящихся в отношении
 называют также противоположным отношением для R. Упражнение. Сформулируйте самостоятельно, что называется
называют также противоположным отношением для R. Упражнение. Сформулируйте самостоятельно, что называется
конъюнкцией и дизъюнкцией отношений. Рассмотрите конъюнкцию, дизъюнкцию и отрицание отношения 
Инверсией бинарного отношения R называется отношение, обозначаемое  и такое, что
и такое, что  тогда и только тогда, когда bRa.
тогда и только тогда, когда bRa.
Понятно, что инверсией отношения  является отношение R, т.е.
является отношение R, т.е.
можно сказать, что отношения  взаимно обратны.
взаимно обратны.
Пример. Инверсией для отношения "больше" является отношение "меньше"; то же - для их разновидностей: старше - моложе, дороже -дешевле, выше - ниже и т.п.
Инверсия отношения отличается от отрицания: инверсией
отношения X > Y на множестве чисел является отношение X < Y, тогда как отрицанием - отношение 
Обратимся теперь к некоторым типам отношений, обладающих свойствами, которые представляют особый интерес.
Рефлексивное (соответственно, антирефлексивное)
отношение- бинарное отношение, обладающее свойством a'.aRa
(соответственно, 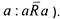
Симметричное отношение - бинарное отношение, обладающее свойством 
Антисимметричное отношение - бинарное отношение такое, что 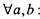 если
если  - т.е. если а и b - в этом порядке! -
- т.е. если а и b - в этом порядке! -
находятся в отношении R, то b и а - нет. Это же свойство выражают иначе:  : если aRb и bRa, то а - b.
: если aRb и bRa, то а - b.
Примеры. 1) Отношения равенства рефлексивны и симметричны.
2) Отношения между парами чисел "больше", "меньше" -антирефлексивны и антисимметричны.
3) Отношение параллельности прямых рефлексивно и симметрично.
Понятие симметрии можно распространить и на отношения большей
арности, имея в виду симметрию для отдельных пар в п -кортеже. Так,
|тернарное отношение R(X,Y,Z) симметрично по паре (F,Z), если
всегда R(a,b,c) выполняется вместе с R(a,c,b). Например, отношение
(X - Y - Z) симметрично по (F,Z). Действительно, если X - Y = Z, то
X = Y + Z и ясно, что перестановка К и Z не изменяет равенства. Транзитивное отношение - бинарное отношение, обладающее
свойством 
Примеры. 1) Отношения "больше" и "меньше" транзитивны. 2} Отношение параллельности прямых транзитивно.
3) Отношения равенства транзитивны.
4) Отношения "правее", "левее" между делениями на линейной шкале прибора
5) Отношения "севернее", "южнее" между точками земной
поверхности
Примеры нетранзитивных отношений.
1) Отношение перпендикулярности прямых.
2) Известное из истории европейского средневековья отношение между вассалом и сюзереном, выражавшееся формулой: "вассал моего вассала - не мой вассал".
3) Отношение между игроками или командами в спортивном
турнире: "участник X выиграл у участника Y ": возможно, что А выиграл
у В, В выиграл у С, но А проиграл С-
4) Отношения "западнее", "восточнее" между точками земной поверхности- Ярославль (40° восточной долготы) западнее Хабаровска (135° восточной долготы); Хабаровск западнее Торонто (80° западной долготы), но Ярославль восточнее Торонто.
Пример. Пусть аБ b - отношение на множестве островов некоторого архипелага, состоящее в том, что остров b является ближайшим для острова а (если допустить, что среди попарных расстояний могут быть равные, то ближайших для а может оказаться
несколько). Отношение Б разумно считать определенным только для пар различных элементов, и, поэтому, нерефлексивным: иначе
ближайшим к каждому острову будет он сам и только он. Отношение Б, вообще говоря, несимметрично, поскольку если b - ближайший для а, то для b ближайшим может оказаться как а, так и какой-то третий остров
с Наконец, отношение Б не является транзитивным, что очевидно, например, для трех островов, расположенных на одной прямой или вообще не в вершинах равностороннего треугольника.
В табл 1 сведены характеристики рассмотренных выше отношений
Я,-Л4-
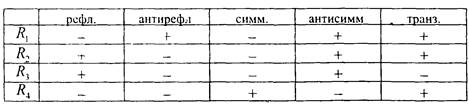
Для рефлексивного (соответственно, антирефлексивного) отношения все диагональные элементы матрицы равны 1 (соответственно, 0), а схема в каждой вершине имеет (соответственно, не имеет) петлю. Матрица симметричного (соответственно, антисимметричного) отношения симметрична относительно главной диагонали, т.е.  (соответственно,
(соответственно, 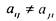 ), а схема вместе с
), а схема вместе с
каждой стрелкой содержит (соответственно, не содержит) противоположно направленную.
Транзитивное замыкание бинарного отношения R есть бинарное отношение 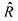 такое, что
такое, что 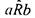 (т е. элементы a,b находятся в
(т е. элементы a,b находятся в
отношении  ), если существует цепочка
), если существует цепочка  , для которой
, для которой
 . Например, для отношения "быть сыном" транзитивным замыканием является отношение "быть прямым потомком по мужской линии". Для отношения на множестве квартир дома "иметь общую стену" транзитивное замыкание - это отношение "находиться на
. Например, для отношения "быть сыном" транзитивным замыканием является отношение "быть прямым потомком по мужской линии". Для отношения на множестве квартир дома "иметь общую стену" транзитивное замыкание - это отношение "находиться на
^ одном этаже". Отношение  , конечно, транзитивно.)
, конечно, транзитивно.)
§4. Отношения эквивалентности "
Отношение эквивалентности - бинарное отношение, являющееся рефлексивным, симметричным и транзитивным.
Примеры. 1) Рассмотренные выше отношения равенства, параллельности прямых.
2) Отношение подобия треугольников.
3) Отношение между элементами множества всех многоугольников: "иметь одинаковое число сторон".
4) Бинарное отношение пропорциональности Р между парами чисел (X, У) и (Z, Т): (X, Y)P(Z,Т), если XIY = ZIT.
5) Упоминавшееся выше отношение между целыми числами -"иметь одинаковые остатки от деления на 7".
Пусть на множестве М введено некоторое отношение эквивалентности R. Для каждого элемента  рассмотрим
рассмотрим
множество 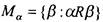 элементов
элементов  , эквивалентных
, эквивалентных  . В силу
. В силу
симметричности и транзитивности отношения R, если  , то
, то
 . Если же
. Если же  ; иначе, если бы существовал
; иначе, если бы существовал
элемент  , то выполнялось бы
, то выполнялось бы  и, в силу
и, в силу
транзитивности 
Таким образом, система различных множеств  - разбиение
- разбиение
множества М (полнота разбиения обусловлена рефлексивностью R), и тем самым, каждое отношение эквивалентности на множестве порождает разбиение этого множества на классы эквивалентности
бинарного отношения R на множестве М - систему подмножеств
множества М такую, что
1) любые два элемента из одного класса эквивалентны;
2) любые два элемента из разных классов не эквивалентны.
Верно и обратное. Любое разбиение множества М можно рассматривать как отношение эквивалентности, в котором находятся пары элементов, отнесенные к одному и тому же классу разбиения, и не находятся элементы из разных классов.
Группировку объектов, применяемую в статистике, законодательстве (например, разделение предприятий на малые, средние и крупные для установления нормативов, единых для всех элементов группы) и в других областях, можно рассматривать как установление эквивалентности.
Классы эквивалентности для примеров 2-5.
(2) - множества подобных друг другу треугольников; в разных классах - треугольники разной формы.
(3) - счетное множество классов: в л -и класс входят все п -угольники.
(4) - пары чисел (X, Y), имеющих одинаковое значение частного X/Y.
(5) - 7 классов чисел  имеющих остаток / при
имеющих остаток / при
делении на 7. Класс Nt содержит числа вида 
Например, для / =4 класс  -этомножество(...-10, -3, 4, 11, 18, 25,..). Рассмотрим еще один важный пример. Определим отношение Э между множествами следующим образом:
-этомножество(...-10, -3, 4, 11, 18, 25,..). Рассмотрим еще один важный пример. Определим отношение Э между множествами следующим образом:  , или короче -
, или короче -
 , если существует взаимно однозначное соответствие между множествами L и М. Можно показать, что Э является отношением эквивалентности. Действительно, если для трех множеств L,M,K выполнено L Э М и М Э К, то элементу
, если существует взаимно однозначное соответствие между множествами L и М. Можно показать, что Э является отношением эквивалентности. Действительно, если для трех множеств L,M,K выполнено L Э М и М Э К, то элементу 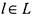 соответствует некоторый
соответствует некоторый
элемент 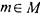 , а элементу т соответствует элемент
, а элементу т соответствует элемент  ; тогда
; тогда
 , поскольку можно сопоставить элементу / элемент k. Классы эквивалентности состоят при этом из множеств, имеющих одинаковую мощность (для конечных множеств - одинаковое число элементов).
, поскольку можно сопоставить элементу / элемент k. Классы эквивалентности состоят при этом из множеств, имеющих одинаковую мощность (для конечных множеств - одинаковое число элементов).
Дата публикования: 2014-11-18; Прочитано: 5288 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
