Определители. Определителем (детерминантом) n-го порядка называется числовая характеристика квадратной матрицы A размера

Определителем (детерминантом) n -го порядка называется числовая характеристика квадратной матрицы A размера 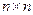, вычисляемая по определенному правилу (см., например, ). Обозначается определитель одним из символов .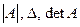

Определитель первого порядка – определитель для матрицы размера 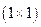, состоящей из одного числа, – равен самому числу:

.

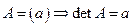Для определителей второго и третьего порядков имеем:

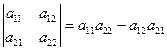; (1)

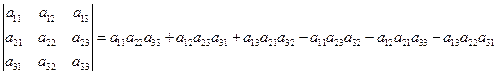. (2)

При вычислении определителя третьего порядка удобно пользоваться следующей схемой (схема Саррюса):

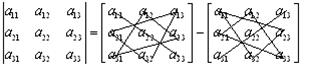
Рис. 2

Определитель равен алгебраической сумме произведений элементов, соединенных на рисунке одной непрерывной линией. Для определителей порядка выше третьего подобных простых схем не составлено, и для вычисления надо использовать упрощения, основанные на свойствах определителей.

Введем несколько важных понятий.

Минором 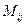определителя 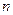−го порядка называется определитель, полученный из данного вычеркиванием 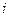−ой строки и 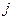−го столбца.

В общем случае минором прямоугольной матрицы называется любой определитель, полученный из нее в результате вычеркивания каких-то строк или столбцов. В частности, сам определитель квадратной матрицы тоже является ее минором. Миноры 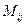выделены в силу их важности для приложений, что видно из формул (3)-(4).

Алгебраическим дополнением к элементу 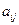определителя 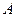называется выражение

.

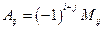Для вычисления определителя 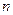−го порядка справедливы рекуррентные формулы через определители (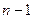)−го порядка:

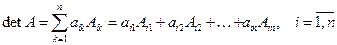(3)

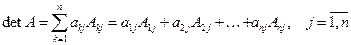. (4)

Формулы (3)-(4) представляют разложение определителя по элементам строки (столбца) и в частности показывают, что определитель не изменяется при перестановке строк со столбцами, т.е. определители исходной матрицы и транспонированной к ней равны.