Проверка адекватности регрессионной модели

Введем обозначения

Среднеквадратическое отклонение результативного признака yi от выровненных 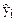. 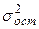– остаточная дисперсия
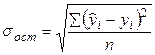
Среднеквадратическое отклонение факторного признака хi от средней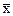
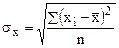
Общая дисперсия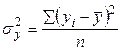
Среднеквадратическое отклонение модельных значений от средней.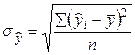
Межгрупповая дисперсия измеряет вариацию групповых средних 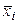вокруг общей средней. Она измеряет вариацию, обусловленную признаком, положенным в основу группировки.

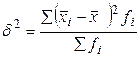
Для проверки з начимости коэффициентов линейной регрессии 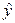= а₀+а₁х при n<30 используют t-критерий Стьюдента. Для этого вычисляют расчетные значения t – критерия

.

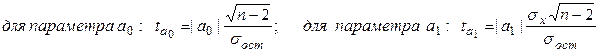Полученные значения 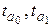сравнивают с критическими t_кр, которые определяют по таблице Стьюдента при заданном уровне значимости a (обычно a=0.05) и числом степеней свободы n=n-m=n-2. Параметр признается значимым, если t_расч > t_кр.

Теснота корреляционной связи между x и y может быть измерена империческим корреляционным отношением 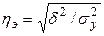(0≤ 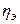≤1). Чем ближе оно к 1, тем теснее связь. При 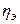=0 связи нет.

Теснота корреляционной связи между x и y для при заданной зависимости определяется индексом корреляции

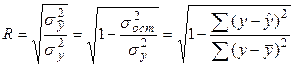(0≤R≤1).

Чем ближе R к 1, тем теснее связь. При R=0 связи нет. Величину R² называют коэффициентом детерминации. Коэффициент детерминации характеризует какая часть общей вариации у объясняется изучаемым фактором х.

Показателем тесноты линейной связи является линейный коэффициент корреляции

(-1≤r≤1).

Величину r2 называют линейным коэффициентом детерминации. Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента. Для этого вычисляют расчетные значения t – критерия

,

где n-2 – число степеней свободы при заданном уровне значимости a (обычно a=0.05). Расчетное значение 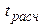сравнивают с табличными значениями t-критерия t_кр, которые определяют по таблице Стьюдента при заданном уровне значимости a (обычно a=0.05) и числом степеней свободы n=n-m=n-2. Параметр r признается значимым, если t_расч > t_кр.