142 Эволюция генетического материала
| Таблица 24.4. Изменение частот аллелей за одно поколение при отборе против рецессивных гомозигот
|
|
|
| Генотип
| Всего
| Частота аллеля а
|
|
| АА
| Аа аа
|
|
|
| 1. Начальная частота зиготы
| 
| 
| 
| 
|
| 2. Приспособленность
(w)
| 
| 
| 
| 
|
| 3. Вклад каждого генотипа в следующее поколение
| 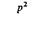
| 
| 
| 
|
| 4. Нормализованная частота
| 
| 
| 
| 
|
| 5. Изменение частоты аллеля
| 
| 
| 
| 
|
получаем относительные эффективности размножения всех генотипов.
Суммируя значения, выписанные в третьей строке таблицы, мы видим, что сумма не равна единице:
 Для того чтобы значения, выписанные в третьей строке таблицы, стали частотами, мы разделим каждое из них на их сумму, как это сделано в четвертой строке таблицы. Сумма новых значений (частот) равна единице:
Частоту
Для того чтобы значения, выписанные в третьей строке таблицы, стали частотами, мы разделим каждое из них на их сумму, как это сделано в четвертой строке таблицы. Сумма новых значений (частот) равна единице:
Частоту  аллеля а после одного поколения отбора q1 можно подсчитать, складывая частоту гомозигот аа с половиной частоты гетерозигот Аа: аллеля а после одного поколения отбора q1 можно подсчитать, складывая частоту гомозигот аа с половиной частоты гетерозигот Аа:
 Частоту аллеля А после одного поколения отбора можно подсчитать либо аналогично, складывая частоту гомозигот
Частоту аллеля А после одного поколения отбора можно подсчитать либо аналогично, складывая частоту гомозигот
| АА с половиной частоты гетерозигот Аа, либо вычитая из единицы частоту аллеля а после отбора. Используя первый прием, получаем
 Изменение частоты аллелей показано в пятой строке таблицы. Начальная частота аллеля а равна q, частота после одного поколения отбора ql — — (q — sq2)/(l — sq2). Следовательно, изменение частоты за одно поколение составляет
Изменение частоты аллелей показано в пятой строке таблицы. Начальная частота аллеля а равна q, частота после одного поколения отбора ql — — (q — sq2)/(l — sq2). Следовательно, изменение частоты за одно поколение составляет
 И так как 1 — q = ρ, окончательно получаем
И так как 1 — q = ρ, окончательно получаем
 Поскольку значения s, p и q всегда положительны (и меньше единицы) или равны нулю, числитель этой дроби либо отрицателен, либо равен нулю. А так как значения s и q меньше единицы, знаменатель - число всегда положительное. Следовательно, Δq -величина отрицательная (или равная нулю), т. е. значение q уменьшается в результате отбора.
Поскольку значения s, p и q всегда положительны (и меньше единицы) или равны нулю, числитель этой дроби либо отрицателен, либо равен нулю. А так как значения s и q меньше единицы, знаменатель - число всегда положительное. Следовательно, Δq -величина отрицательная (или равная нулю), т. е. значение q уменьшается в результате отбора.
|









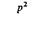











 Для того чтобы значения, выписанные в третьей строке таблицы, стали частотами, мы разделим каждое из них на их сумму, как это сделано в четвертой строке таблицы. Сумма новых значений (частот) равна единице:
Частоту
Для того чтобы значения, выписанные в третьей строке таблицы, стали частотами, мы разделим каждое из них на их сумму, как это сделано в четвертой строке таблицы. Сумма новых значений (частот) равна единице:
Частоту  аллеля а после одного поколения отбора q1 можно подсчитать, складывая частоту гомозигот аа с половиной частоты гетерозигот Аа:
аллеля а после одного поколения отбора q1 можно подсчитать, складывая частоту гомозигот аа с половиной частоты гетерозигот Аа:
 Частоту аллеля А после одного поколения отбора можно подсчитать либо аналогично, складывая частоту гомозигот
Частоту аллеля А после одного поколения отбора можно подсчитать либо аналогично, складывая частоту гомозигот
 Изменение частоты аллелей показано в пятой строке таблицы. Начальная частота аллеля а равна q, частота после одного поколения отбора ql — — (q — sq2)/(l — sq2). Следовательно, изменение частоты за одно поколение составляет
Изменение частоты аллелей показано в пятой строке таблицы. Начальная частота аллеля а равна q, частота после одного поколения отбора ql — — (q — sq2)/(l — sq2). Следовательно, изменение частоты за одно поколение составляет
 И так как 1 — q = ρ, окончательно получаем
И так как 1 — q = ρ, окончательно получаем
 Поскольку значения s, p и q всегда положительны (и меньше единицы) или равны нулю, числитель этой дроби либо отрицателен, либо равен нулю. А так как значения s и q меньше единицы, знаменатель - число всегда положительное. Следовательно, Δq -величина отрицательная (или равная нулю), т. е. значение q уменьшается в результате отбора.
Поскольку значения s, p и q всегда положительны (и меньше единицы) или равны нулю, числитель этой дроби либо отрицателен, либо равен нулю. А так как значения s и q меньше единицы, знаменатель - число всегда положительное. Следовательно, Δq -величина отрицательная (или равная нулю), т. е. значение q уменьшается в результате отбора.
