24. Естественный отбор 141
| Дополнение 24.1. Типы равновесий
|
| Система находится в равновесии, если ее состояние не изменяется без вмешательства внешних сил. Равновесие может быть устойчивым, неустойчивым и безразличным (нейтральным) в зависимости от того, как ведет себя система, выведенная из состояния равновесия. Устойчивым равновесие называется в том случае, когда система, выведенная из равновесия, возвращается в исходное состояние. Равновесие неустойчиво, если после устранения возмущающего воздействия система продолжает удаляться от равновесия в направлении возмущения (до тех пор, пока не достигнет естественных границ). Равновесие безразлично (нейтрально), когда состояние системы, после устранения возмущающего воздействия не изменяется (т.е. система никак не реагирует на возмущение).
| Механические модели, иллюстрирующие равновесие этих трех типов, изображены на рис. 24.1: шарик в нижней точке гладкой вогнутой поверхности находится в состоянии устойчивого равновесия, шарик на вершине выпуклой поверхности - в состоянии неустойчивого равновесия, а шарик на абсолютно горизонтальной поверхности -в состоянии безразличного равновесия.
Равновесие всех этих трех типов может реализовываться в отношении частот аллелей. В равновесном состоянии в популяции может присутствовать лишь один аллель данного локуса (мономорфное равновесие) или более одного аллеля (полиморфное равновесие).
|
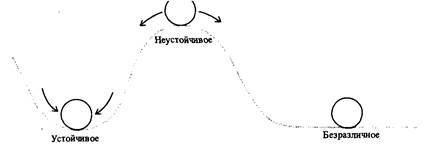
|
| Рис. 24.1. Равновесие трех типов. Шарик, выведенный из состояния устойчивого (слева) к неустойчивого (посредине) равновесия и предоставленный самому себе, движется в направлениях, указанных стрелками. В случае безразличного равновесия (справа) шарик остается там, где он оказался после воздействия на него внешней силы.
|
| Дополнение 24.2. Отбор против рецессивных гомозигот
|
| Модель отбора против рецессивных гомозигот рассмотрена в основном тексте. Главные этапы расчета изменения частоты аллеля на протяжении одного поколения действия отбора представлены в табл. 24.4. Сначала (на стадии зигот) частоты двух аллелей, А и а, равны соответственно p и q. Предполагается, что частоты генотипов отвечают закону Хар-
| ди — Вайнберга; они выписаны в первой строке таблицы. Поскольку присутствуют лишь два аллеля данного локуса, то p + q = 1 и, следовательно, р2 + 2pq + + q2 = (p + q)2 = 1. Основной этап расчета представлен в третьей строке таблицы: исходные частоты зигот (первая строка) умножаются на их приспособленности (вторая строка). В результате мы
|


