 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 3. Пер. с англ.: – М.: Мир, 1988. – 336 с. LM равна сумме удвоенного числа индивидуумов с генотипом LM LM и числа индивидуумов с генотипом LM LN
|
|
114 Эволюция генетического материала
| Таблица 23.4. Равновесие Харди — Вайнберга для трех аллелей | |||
| Частоты гамет у самок | |||
| Частоты гамет у самцов | |||
| p (A 1) | q(А2) | r (A 3 ) | |
| p (А 1) | р 2(A1A1) | pq(A1A 2 ) | рr(А 1 А 3 ) |
| q(A2) | pq(A1A2) | q2(A2A2) | qr(A2A3) |
| r(А3) | pr(AlA3) | qr(A2A3) | r2(A3A3) |
LM равна сумме удвоенного числа индивидуумов с генотипом LM LM и числа индивидуумов с генотипом LM LN, деленной на общее число аллелей в выборке (т.е. на удвоенное число обследованных лиц). Таким образом, частота аллеля LM равна (1787·2) +3039)/(2·6129) = 0,5395. Точно так же можно рассчитать частоту аллеля LN; она равна 0,4605. Тогда отношение теоретически ожидаемых равновесных частот генотипов, рассчитанное в соответствии с законом Харди—Вайнберга, составляет 0,2911 LMLM:0,4968 LM LN: 0,2121 LN LN, что очень близко к реальному отношению генотипических частот, наблюдаемых в популяции (0,292:0,496:0,213).
Только что приведенный способ рассуждения в отношении двух аллелей можно применить для демонстрации справедливости закона Харди—Вайнберга для любого числа аллелей. В табл. 23.4 показаны равновесные частоты генотипов для локуса с тремя аллелями, представленными в популяции с частотами p, q и r, так что p + q + r = 1. На рис. 23.2 изображена геометрическая интерпретация этого случая на примере групп крови системы АВО, определяемых одним локусом с тремя аллелями.
| Рис. 23.2. Геометрическое представление взаимосвязи между частотами аллелей и частотами генотипов для генов, определяющих системы групп крови АВО. | 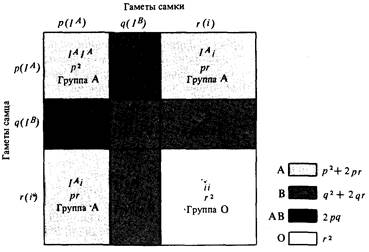
|
Дата публикования: 2014-11-18; Прочитано: 614 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
