Основные модели экономического роста

История развития экономики и экономической науки связаны с попытками экономистов понять и объяснить причины динамичного или сдерживающего развития экономических систем, роста благосостояния одних и бедности других. Это нашло отражение в разработке различных теорий и моделей экономического роста.

Модели экономического роста, как и любые модели, представляют собой абстрактное, упрощённое выражение реального экономического процесса в форме уравнений, графиков, таблиц и т.д. Ряд допущений, предваряющих каждую модель, уже изначально отодвигает результат от реальных процессов, но, тем не менее, даёт возможность проанализировать отдельные стороны и закономерности такого непростого явления, как экономический рост.

По сравнению со статистическими моделями равновесия, предназначенными для выяснения условий достижения равновесного состояния, целью разработки модели равновесия экономического роста является определение условий, при которых возможно подержание равновесия в процессе развития. Это так называемые трендовые траектории, вдоль которых, отклоняясь в ту или иную сторону, двигается реальная экономика.

В моделях равновесного роста выделяют устойчивые и неустойчивые траектории развития. Устойчивые траектории – это такие равновесные траектории, отклоняясь от которых экономика по истечении некоторого периода развития вновь возвращается к равновесию. Неустойчивые траектории – это такие равновесные траектории сбалансированного роста, по которым экономика, однажды достигнув равновесия, может двигаться сколь угодно долго, если не изменяются её внутренняя структура или исходные условия развития.

Модели равновесного роста предназначены для изучения свойств равновесных траекторий (их устойчивости или неустойчивости), а также для определения условий, возвращающих экономическую систему, на равновесную траекторию в случае отклонения. Эти модели следует отличать от моделей роста, ориентированных на прогноз тенденций изменения реальных экономических систем.

Основное назначение разработки моделей экономического роста состоит в том, что, с одной стороны, на их основе осуществляются аналитические работы, а с другой – они позволяют прогнозировать макроэкономические процессы.

Первые разработки макроэкономических моделей экономического роста относятся к 1758 году, когда Ф. Кенэ создал свои “Экономические таблицы”, в которых он впервые выдвинул понятие “продукта общества”, показал его движение между основными классами (фермеры-арендаторы земли, ремесленники и торговцы, землевладельцы); высказал идею наличия “экономического излишка”, который присваивался королём и церковью.

А. Смит, Д. Рикардо, К. Маркс, несмотря на различные подходы, рассматривали капитал как определяющую роль в теории роста экономики.

В современной экономической литературе выделяют следующие основные модели экономического роста:

- неокейнсианские,

- неоклассические,

- “затраты - выпуск”.

1. Неокейнсианские модели.

Е. Домар, американский экономист и Г. Харрод, английский экономист, ведущие теоретики неокейнсианского направления, развили теорию Д. Кейнса, исследовали проблемы динамики совокупного спроса, использование инвестиций, понятие мультипликатора. Они исходили из главной идеи Кейнса, развитое им в работе “Общая теория занятости, процента и денег”, в которой определена главенствующая роль спроса в обеспечении макроэкономического развития. Решающий элемент спроса – инвестиции, которые посредством мультипликатора увеличивают прибыль. Одновременно они сами (спрос, инвестиции) вызваны ростом прибыли, так как капитальные вложения представляют собой функцию увеличения прибыли.

Модель экономического роста Е. Домара

Рассматривая модель, в которой инвестиции выступают не только фактором создания дохода, но и новых производственных мощностей. Динамическая сбалансированность спроса и предложения определяется динамикой капитальных вложений, которые образуют новые мощности и новые доходы. Поэтому, задача сводится к определению объёма и динамики инвестиции. Домар предложил для решения систему из трёх уравнений: уравнение предложения, уравнение спроса, уравнение спроса и предложения совместно.

Уравнение предложения: dx = I×G, где dx - прирост производства, I – объём капитальных вложений, G – средняя производительность капитальных вложений.

Уравнение спроса: М = 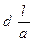, где а – средняя склонность к сбережениям, обратная величина которой определяет величину мультипликатора, I – объём капиталовложений.

В данном уравнении учитывается лишь прирост инвестиций. Основное уравнение макроэкономического роста – равенства между приростом доходов и приростом производства: 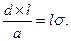Исходя из него, получаем норму прироста капитальных инвестиций. Модель Домара однофакторная и однопродуктовая. В ней учтены лишь инвестиции и один продукт.

Модель экономического роста Р. Харрода.

Модель Р. Харрода выступает развитием модели Е. Домара. Как и в ней, в модели Харрода норма уравновешенного роста является функцией соотношения роста доходов и капитальных вложений. Это дало повод называть эти модели моделями Харрода-Домара. Вместе с тем, если модель Домара базируется на использовании принципа мультипликатора, то в основе модели Харрода лежит принцип акселератора, состоящей в том, что рост инвестиций является ускоренным по сравнению с ростом национального дохода и потребительского спроса. Каждый прирост дохода порождает большой прирост новых инвестиций:

,

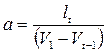где а – акселератор, 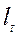– новые инвестиции за данный период времени,

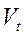– доход за данный период, 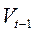– доход за предшествующий период.

Таким образом, прирост инвестиций равняется произведению прироста дохода на акселератор:

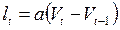
Модель Харрода показывает, что путём установления на должном уровне нормы накопления (доли дохода идущей на сбережения) может быть достигнут устойчивый экономический рост на неограниченное будущее.

2. Неоклассические модели.

Неоклассические модели экономического роста строятся на базе производственной функции и основаны на предпосылках полной занятости, гибкости цен на всех рынках и полной взаимозаменяемости факторов производства.

Модель производственной функции Кобба-Дугласа.

Модель создана американским экономистом П. Дугласом и американским математиком Х. Кобба. Важнейшие черты функции Кобба-Дугласа формируются следующим образом:

1. предполагается постоянство прибыли и удельных расходов, отсутствие накопления, сумма эластичности производства (труд и капитал) равна единице. Степень взаимозаменяемости факторов колеблется от 0 до 1 и обычно менее единицы. Пределы взаимозаменяемости ставит данный уровень технического развития;

2. теоретически возможна безграничная замена труда капиталом;

3. функция не учитывает изменения качества производственных факторов. Функция приемлема только для экстенсивного экономического роста.

Функция Кобба-Дугласа получена в результате математического преобразования простейшей производственной функцией Y=F(L,) в такую модель, которая показывает, какой долей совокупного продукта вознаграждается участвующий в его создании фактор производства. Она имеет следующий вид:

Y = A 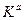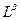, где a изменяется в пределах от 0 до 1, а β = l-a

Параметр А – коэффициент, отражающий уровень технологической производственности и в краткосрочном периоде он не изменяется.

Показатели a и β – коэффициенты эластичности объемов выпуска (V) по фактору производства, то есть по капиталу (K) и труду (L) соответственно. При этом, если каждый из факторов оплачивается в соответствии со своим предельным продуктом, то a и β показывают доли капитала и труда в совокупном доходе. То есть, если цена капитала равна предельному продукту капитала, а цена труда равна предельному продукту труда, то параметры a и β определяют пропорцию, в которой труд и капитал получают свое вознаграждение за созданный продукт, то есть долю капитала в доходе AV и долю труда в доходе βV.

Основные свойства производственной функции Кобба-Дугласа:

Первое свойство – постоянство отдачи от масштаба, то есть, если увеличить использование капитала и труда в N раз, то объем совокупного выпуска, или объем дохода возрастает в такое же число раз.

Второе свойство – связано с изменением предельной производительности факторов. Если привлечь в производство дополнительное количество капитала К, а труд L использовать в прежнем объёме то, при прочих равных условиях, предельная производительность труда увеличиться, а предельная производительность возросшего объёма капитала снизиться. Если же увеличить количество труда, при прочих равных условиях, то его предельная производительность снизиться, а предельная производительность капитала возрастёт. Таким образом, нарушение пропорции между трудом и капиталом при заданной технологии приводит к отклонению от оптимального объёма производства, то есть к его неэффективности.

Третье свойство – постоянство отношения дохода от труда к доходу от капитала (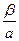), то есть постоянство соотношения доли капитала и труда национальном продукте.

Неоклассические модели обосновывают устойчивость равновесного роста в длительном периоде. В них основной методологической предпосылкой являются наличие совершенной конкуренции, автоматическое восстановление общего макроэкономического равновесия за счёт гибкости цен, поддержание полной занятости и полное использование производственных мощностей, позволяющих экономике развиваться темпами, которые определяются динамикой факторов производства.

Модель экономического роста Р. Солоу

Автором модели является американский экономист, лауреат Нобелевской премии по экономике (1987 год) за вклад в теорию экономического роста.

Модель выявляет механизм влияния сбережения, роста трудовых ресурсов и научно-технического прогресса на уровень жизни населения и его динамику. Модель является простой, так как в ней представлены только домохозяйства и фирмы.

В модели использована производственная функция Кобба-Дугласа, в которой труд и капитал являются субъинститутами, определено соотношение этих факторов и показано его изменение в процессе экономического роста. Другими предпосылками анализа в модели Солоу являются:

- убывающая предельная производительность капитала;

- постоянная отдача от масштаба цен;

- постоянная норма выбытия;

- отсутствие инвестиционных лагов;

Необходимым условием равновесного состояния экономической системы выступает равенство совокупного спроса и совокупного предложения.

Солоу предложил формулу, известную в современной экономической науке как “золотое правило накопления”. В соответствии с ним выбытие капитала не может быть (не должно быть) больше, чем предельный продукт, созданный функционирующим капиталом. Выбытие капитала не может быть (не должно быть) больше чем предельная склонность к инвестициям.

“Золотое правило” показывает уровень капиталовооружённости, оптимальный (при данных условиях) для потребления (max ).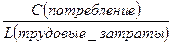

“Золотое правило” определяет запас капитала, необходимый для устойчивого состояния экономики с наивысшим уровнем потребления. Наивысшее потребление определяется не величиной (как можно больше) капитала, а его оптимальным размером. В стационарном состоянии инвестиции равны покрытию износа.

Практические выводы:

1. Определена прямая зависимость между S (сбережения) → I (инвестиции) → К (капитал) → Q (ВВП) в долгосрочном периоде.

2. Оптимум С (потребление) есть функция 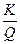, но для достижения оптимума необходимы инвестиции, то есть ограничения потребления (C) и государственное стимулирование (I).

3. Равновесие S = I на практике нарушается, так как факторы, определяющие S не совпадают с факторами, от которых зависит I.

4. Формулу S = gx 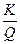, где g – естественный прирост трудовых затрат, 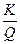– капиталовооружённость при сохранении той же пропорции между K и Q, можно преобразовать g= 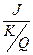. Прирост трудовых затрат не должен превышать пределов, поставленных S и 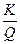. Чем выше, при прочих неизменных условиях, прирост населения (предложения труда) тем ниже объём Q, приходящийся на одного занятого.

5. Если потребление осуществляется за счёт инвестиций, то это грозит свёртыванию выпуска ВВП. Выход связан с перспективами технологического прогресса, в невостребованном потенциале ресурсов.

3. Модель “затраты – выпуск”

Американский экономист российского происхождения В. Леонтьев, представитель неоклассицизма, лауреат нобелевской премии по экономике (1973 г.) впервые разработал модель “затраты – выпуск”, получившее название модель межотраслевого баланса и леонтьевского типа. В её основе положен разработанный им метод экономико-математического анализа “затраты - выпуск”, использование которого дало возможность исследовать межотраслевые взаимосвязи и взаимозависимости между отраслями экономики, которые могут проявляться во взаимовлиянии цен, объёма производства, инвестиций, доходов и т. п.

Анализ по методу “затраты – выпуск” связан с построением шахматных таблиц (шахматных балансов). В них предполагается, что произведённый продукт по натурально-вещественной структуре подразделяется на промежуточный и конечный. В зависимости от того, как учитывается состав конечного продукта, в модели может отражаться (или не отражаться) объём инвестиции, а следовательно, и воспроизводственные возможности в будущих периодах, то есть модели могут учитывать фактор времени при динамическом типе или не учитывать статистический тип.

В настоящее время отчётные межотраслевые балансы вместе с системой национальных счетов составляет базу для аналитических расчётов. С их помощью исследуются конкретные экономические проблемы:

- структура экономики и темп экономического роста;

- соотношение возможных изменений налогов, заработной платы, цены и прибыли;

- межотраслевые производственные связи и важнейшие экономические пропорции в экономике.

С помощью моделей можно оценить влияние различных вариантов экономической политики на экономический рост.