 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Тема 5 Линейные операции над векторами. Скалярное произведение векторов
|
|
КОНСПЕКТ 5
5.1 КООРДИНАТЫ В ПРОСТРАНСТВЕ
Теперь рассмотрим векторы в трехмерном пространстве, здесь практически всё так же, КАК НА ПЛОСКОСТИ! Только добавится ещё одна координата. Трехмерные чертежи выполнять тяжко, поэтому ограничимся одним вектором, который для простоты отложим от начала координат:
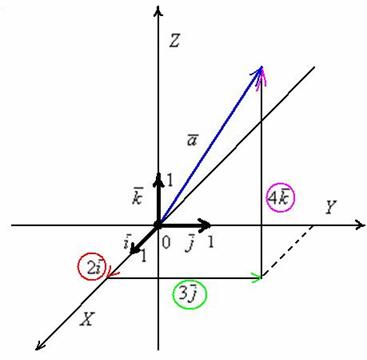
Перед вами ортонормированный базис 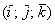 трехмерного пространства и прямоугольная система координат, единичные векторы
трехмерного пространства и прямоугольная система координат, единичные векторы 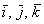 данного базиса попарно ортогональны:
данного базиса попарно ортогональны: 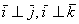 и
и 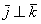 . Ось
. Ось 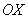 наклонена под углом 45 градусов только для того, чтобы складывалось визуальное впечатление пространства.
наклонена под углом 45 градусов только для того, чтобы складывалось визуальное впечатление пространства.
Любой вектор 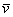 трехмерного пространства можно единственным способом разложить по ортонормированному базису
трехмерного пространства можно единственным способом разложить по ортонормированному базису 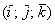 :
:
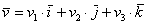 , где
, где 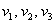 – координаты вектора
– координаты вектора 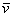 (числа) в данном базисе.
(числа) в данном базисе.
Пример с картинки: 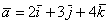 . Давайте посмотрим, как здесь работают правила действий с векторами. Во-первых, умножение вектора на число:
. Давайте посмотрим, как здесь работают правила действий с векторами. Во-первых, умножение вектора на число: 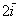 (красная стрелка),
(красная стрелка), 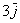 (зеленая стрелка) и
(зеленая стрелка) и 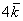 (малиновая стрелка). Во-вторых, перед вами пример сложения нескольких, в данном случае трёх, векторов:
(малиновая стрелка). Во-вторых, перед вами пример сложения нескольких, в данном случае трёх, векторов: 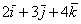 . Вектор суммы
. Вектор суммы 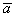 начинается в исходной точке отправления (начало вектора
начинается в исходной точке отправления (начало вектора 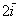 ) и утыкается в итоговую точку прибытия (конец вектора
) и утыкается в итоговую точку прибытия (конец вектора 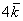 ).
).
Все векторы трехмерного пространства, естественно, тоже свободны, попробуйте мысленно отложить вектор 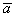 от любой другой точки, и вы поймёте, что его разложение
от любой другой точки, и вы поймёте, что его разложение 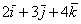 «останется при нём».
«останется при нём».
Аналогично плоскому случаю, помимо записи 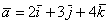 широко используются версии со скобками:
широко используются версии со скобками: 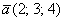 либо
либо 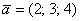 .
.
Если в разложении отсутствует один (или два) координатных вектора, то вместо них ставятся нули. Примеры:
вектор 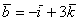 (дотошно
(дотошно 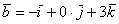 ) – запишем
) – запишем 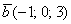 ;
;
вектор 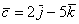 (дотошно
(дотошно 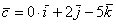 ) – запишем
) – запишем 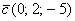 ;
;
вектор 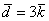 (дотошно
(дотошно 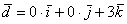 ) – запишем
) – запишем 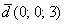 .
.
Базисные векторы записываются следующим образом:
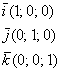
Дата публикования: 2014-11-03; Прочитано: 989 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
