Функции 1 страница

Теорема 2. Любую булеву функцию можно выразить через &, V и отрицание.

Доказательство.

1) Предположим, что булева функция f(x₁, x₂, x₃) есть константа:

2) 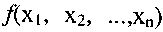произвольная функция, тогда на основании теоремы 1 запишем разложение этой функции по всем n переменным:

Такая форма представления булевой функции называется совершенной дизъюнктивной нормальной

формой.

Пример. Булева функция задана в виде таблицы истинности (см. табл. 1). Записать ее СДНФ.

Таблица 1

X1	X2	X3	f (x1, x2, x3)

Для двоичных наборов, на которых функция равна 1, составляем элементарные конъюнкции (&) и соединяем их знаками дизъюнкции (V), при этом получаем:

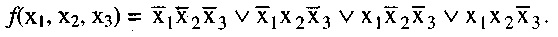
СДНФ

Любую булеву функцию, кроме можно представить конъюнкцией элементарных дизъюнкций.

С этой целью разложим в СДНФ:

Те элементарные дизъюнкции, в которых , можно отбросить (точнее они обратятся в 1), поэтому получим выражение:

которое называется совершенной конъюнктивной нормальной формой.

Пример. Для функции заданной выше таблицей истинности, СКНФ имеет вид:

Из сказанного следует, что каждую булеву функцию можно представить в любой из двух нормальных форм. Исключение составляют функции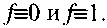

Рассмотрим алгоритм перехода от СДНФ к СКНФ без таблицы истинности.

Для перехода от СДНФ некоторой булевой функции к СКНФ этой функции необходимо:

а) образовать дизъюнкцию дизъюнктивных членов, не входящих в СДНФ;

б) поменять местами символы & и V, а аргументы заменить их отрицаниями.

Аналогичным способом осуществляется переход от СКНФ к СДНФ.

Пример. Пусть дана функция:

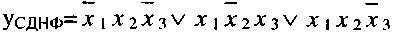
Найти ее СКНФ.

а) образуем дизъюнкцию дизъюнктивных членов, не входящих в СДНФ:

б) СКНФ функции y запишется в виде:

1.3. Каноническая форма булевой функции в алгебре Жегалкина

В алгебре Жегалкина роль совершенных форм играют специальные полиномы, которые принято называть каноническими.

Каноническим полиномом называется конечная сумма по модулю 2 попарно различных конъюнкций переменных таких, что в одной и той же конъюнкции никакая переменная не встречается более одного раза.

Например, выражения:

являются каноническими полиномами,

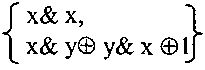не являются каноническими полиномами.

Теорема 3. Любую булеву функцию в алгебре Жегалкина можно представить в виде канонического полинома (полинома Жегалкина).

где причем

Для доказательства заметим, что любая булева функция (кроме представима в СДНФ в булевой алгебре.

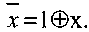Введём расширенную алгебру с операциями (&, V, Тогда в СДНФ без изменения булевой функции можно заменить все знаки V на Далее, все отрицания, встречающиеся в дизъюнктивных членах, заменить выражениями После этого, учитывая

дистрибутивность & относительно , прейдем к выражению булевой функции в виде канонического полинома в алгебре Жегалкина. Теорема, таким образом, будет доказана.

Пример. Дана функция в СДНФ. Представить

ее в канонической форме.

Этот метод получения полинома Жегалкина называется методом подстановки и преобразования.

Существует второй метод получения полинома Жегалкина - метод неопределенных коэффициентов.

Рассмотрим его на примере.

Пример. Выразить в виде полинома Жегалкина.

(полином Жегалкина для функции от 2-х переменных, имеет число членов

Неизвестные коэффициенты 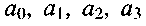вычисляем следующим образом:

при

при

при

при

Получаем полином Жегалкина для заданной булевой функции:

Контрольные вопросы

1. Какое представление булевой функции принято называть «разложением булевой функции по m переменным»? Приведите примеры.

2. Что называют совершенной дизъюнктивной нормальной формой (СДНФ) булевой функции? Поясните на примере.

3. Какое представление булевой функции называют совершенной конъюнктивной нормальной формой (СКНФ)?

4. Как выполнить переход от СДНФ к СКНФ?

5. Что называют каноническим полиномом? Приведите примеры.

6. Запишите полином Жегалкина (канонический полином) для функции

7. Какие методы получения полинома Жегалкина Вы знаете?

2. ПОЛНОТА СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ

Определение. Система S булевых функций называется функционально полной, если для любой булевой функции можно построить равную ей булеву функцию, представляющую собой результат суперпозиции переменных и функций системы S.

Суперпозицией булевых функций называется подстановка одних булевых функций вместо аргументов в другие булевы функции.

Возможность такой подстановки обусловлена тем, что области значений булевых функций и области значений их аргументов совпадают.

Определение. Система S булевых функций называется ослаблено функционально полной, если для

любой булевой функции можно построить равную ей функцию, представляющую собой результат суперпозиции переменных констант 0 и 1 и функций системы S.

При установлении необходимых и достаточных условий функциональной полноты (найденных впервые Э.Постом) большую роль играют пять классов булевых функций, замкнутых относительно суперпозиции.

Первый класс К_о составляют функции, сохраняющие константу 0, т.е. такие функции, которые на нулевом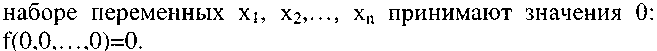

Примеры: и другие,

Суперпозиция любого числа булевых функций, сохраняющих константу 0, является также функцией, сохраняющей константу 0, т.е. К_о - замкнутый класс относительно операции суперпозиции.

Второй класс K₁ составляют функции, сохраняющие 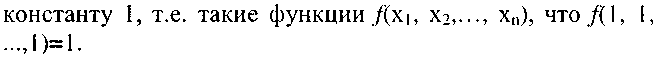Примеры:

Класс К₁ является замкнутым относительно операции суперпозиции.

Третий класс Кс составляют самодвойственные функции. Функция алгебры логики является самодвойственной, если на каждой паре противоположных наборов она принимает противоположные значения, т.е.

Примеры:

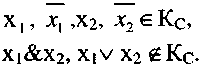
Класс К _с - замкнутый класс.

Четвёртый класс Кл булевых функций составляют ее каноническим полиномом, в ней не окажется членов выше первой степени, т.е. полином имеет вид:

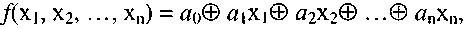
где причём

Примеры:

Класс Кл - замкнутый класс, т.к. суперпозиция любого числа булевых функций этого класса представляет собой линейную функцию.

Пятый класс К_м булевых функций составляют так называемые монотонные функции. Предварительно определим отношение < на наборах. Для любых двух наборов 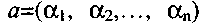и одинаковой размерности отношение 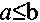эквивалентно отношениям 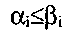для всех

Пример: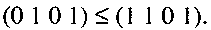

Булева функция называется монотонной, если для любых наборов и таких, что имеет место неравенство:

Иными словами, булева функция называется монотонной, если при любом возрастании набора, значения этой функции не убывают.

Примеры:

Суперпозиция любого числа монотонных булевых функций является монотонной функцией, т.е. класс Км - замкнутый класс.

В таблице 2 приводится разбиение булевых функций от двух переменных на пять классов.

Таблица 2

	Наборы x1, x2	Классы
Функция					K0	K1	Кc	Кл	Км
					+	-	-	+	+
					+	+	-	-	+
					+	-	-	-	-
					+	+	+	+	+
					+	-	-	-	-
				I	+	+	+	+	+
					+	-	-	+	-
					+	+	-	-	+
					-	-	-	-	-
					-	+	-	+	-
					-	-	+	+	-
					-	+	-	-	-
					-	-	+	+	-
					-	+	-	-	-
					-	-	-	-	-
					-	+	-	+	+

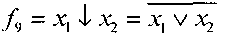
Теорема о функциональной полноте. Для того, чтобы система S булевых функций была функционально полной, необходимо и достаточно, чтобы эта система содержала хотя бы одну функцию, не сохраняющую const 0, хотя бы одну функцию, не сохраняющую const 1, хотя бы одну

нелинейную функцию и хотя бы одну немонотонную функцию.

Если некоторая система булевых функций включает константы 0 и 1, то это означает, что система содержит функцию, не сохраняющую константу 0, функцию, не сохраняющую константу 1, и содержит несамодвойственную функцию. Вместе с тем, константы являются линейными и монотонными функциями. Поэтому имеет место теорема об ослабленной функциональной полноте: для того, чтобы система булевых функций была ослаблено функционально полной, необходимо и достаточно, чтобы эта система содержала хотя бы одну нелинейную и хотя бы одну немонотонную функции.

Из таблицы разбиения булевых функций от 2-х переменных на классы (см. табл. 2) видно, что функции являются функциями, не принадлежащими ни к одному из пяти классов булевых функций. Следовательно, каждая из них образует полную систему булевых функций и на основе каждой из этих функций могут быть построены любые булевы функции n аргументов.

Существуют и другие функционально полные системы булевых функций:

Естественно возникает вопрос, какие из функционально полных систем представляют наибольший практический интерес.

С точки зрения простоты физической реализации и минимальных затрат на оборудование при построении сложных комбинационных схем на практике выбирается избыточный базис булевых функций. Он включает следующие булевы функции:

Контрольные вопросы

1. Какая система булевых функций называется функционально полной?

2. Что называют суперпозицией булевых функций?

3. Какую систему булевых функций называют ослаблено функционально полной?

4. Назовите пять классов булевых функций, замкнутых относительно операции суперпозиции.

5. Приведите примеры булевых функций, относящихся одновременно к классу линейных и классу монотонных булевых функций.

6. Какие булевы функции относятся к классу самодвойственных?

7. Приведите примеры функционально полных систем булевых функций.

3. МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ

3.1. Постановка задачи минимизации булевых функций в классе ДНФ (КНФ)

Известно, что всякая булева функция отличная от 0 и 1, может быть представлена в СДНФ и в СКНФ. Однако, как показывают примеры, очень часто совершенная нормальная форма допускает упрощения, при которых получается эквивалентное выражение, но содержащее меньшее количество букв.

Определение. Конъюнкция называется элементарной, если она является произведением переменных из множества n переменных, причем каждая из r переменных входит в произведение с инверсией или без инверсии не более одного раза, т.е.

Число сомножителей называется рангом элементарной конъюнкции.

Конъюнкция считается элементарной конъюнкцией 0-го ранга.

Дизъюнкция элементарных конъюнкций ненулевого ранга называется дизъюнктивной нормальной формой (ДНФ) булевой функции.

Аналогично определяется понятие элементарной дизъюнкции и конъюнктивной нормальной формы (КНФ) булевой функции.

Примеры:

Определение. ДНФ (КНФ) называется минимальной, если она включает минимальное число букв по сравнению с другими эквивалентными ей ДНФ (КНФ).

Одной из важных задач булевой алгебры является нахождение минимальной формы булевой функции. Известны различные методы минимизации: Квайна, Квайна-Мак-Класки, Блэйка, Вейча, Яблонского-Журавлева и другие.

Упрощение СДНФ осуществляется с помощью преобразований:

(склеивание),

(поглощение),

(вынесение за скобки).

Упрощение СКНФ осуществляется с помощью аналогичных преобразований:

Преобразования а), б) не выводят булеву функцию из класса нормальных форм, а преобразование в) выводит.

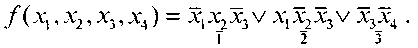
2 Этап. Построение импликантной таблицы для определения всех тупиковых форм.

Таблица 3

Простые импликанты	Исходные импликанты
	*	*
				*	*
		*	*	*		*

После того, как построена импликантная таблица (см. табл. 3), надо найти минимальное покрытие простыми импликантами всех исходных импликант булевой функции.

В данном примере минимальное покрытие включает все простые импликанты, т.е. минимальная ДНФ совпадает с СКДНФ.

Пример 2. Пусть дана булева функция:

Найти min ДНФ. Решение.

1) Определяем изолированные конъюнкции 3-го ранга. Таких нет.

2) Проводим склеивание:

3) Определяем изолированные конъюнкции 2-го ранга. Оказывается, все конъюнкции 2-го ранга изолированные, склеивание производить нельзя.

Сокращенная ДНФ:

4) Строим импликантную таблицу (см. табл. 4).

Простые импликанты		Исходные импликанты одные i шплика нты
	*	*
	*		*
		*		*
			*		*
				*		*
					*	*

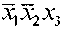
Таблица 4

Имеем 2 тупиковые формы:

Обе тупиковые формы являются минимальными, т.к. число входящих в них переменных одинаково.

3.3. Минимизация булевых функций с помощью диаграмм Вейча (карт Карно)

Рассмотренный выше метод минимизации является аналитическим методом. На практике иногда оказывается более удобным использование графического метода минимизации - метода диаграмм Вейча.

Основная идея этого метода минимизации заключается в том, что исходная булева функция, заданная в виде СДНФ или СКНФ, представляется в форме специальной таблицы, на которой определяется понятие правильной конфигурации и отыскивается минимальное

накрытие всех единиц таблицы системой правильных конфигураций. В результате этого находится минимальная ДНФ исходной функции.

С помощью этого метода обычно минимизируют булевы функции до семи переменных. Если же функция зависит более, чем от семи переменных, то целесообразно использовать аналитические методы минимизации и решение выполнять с помощью ЭВМ.

Диаграмма Вейча для функции от двух переменных, заданных в СДНФ, имеет вид, показанный на рис. 1.

В клетки записываются единицы и нули в соответствии с наборами аргументов, на которых определена функция. Пара единиц в двух соседних клетках по вертикали или по горизонтали выражается одной переменной, т.к. по другой происходит склеивание (см. рис. 2, 3, 4).