Аналіз часових рядів економічних показників і побудова економетричних моделей динаміки

Прикладами часових рядів є щомісячна, щоквартальна, щорічна собівартість перевезення пасажирів, обсяг пасажирів, що перевозяться по депо. Вихідні дані слід формувати по кожному з об'єктів у зв'язку з тим, що інформація буде більш достовірною ніж по групі об'єктів.

Маючи в розпорядженні свій часовий ряд для досліджуваного показника і для всіх чинників, треба перш за все виявити загальну тенденцію зміни цих величин (тренд, еволюційну складову, лінію рівняння).

Як показує дослідження економічних часових рядів, в них завжди міститься загальна тенденція, яку необхідно виявити. Співвідношення У=d(t) можна відшукувати безпосередньо за звітними або дослідженими даними, за К- членним ковзаним середнім.

Використання ковзаних середніх доцільне в разі достатньо довгого ряду. Число членів ковзаної середньої повинно бути обумовлено міркуваннями щодо суті процесу і залежно від кроку часового ряду.

При згладжуванні за допомогою ковзаних середніх доводиться втрачати частину даних: при тричленному вирівнюванні – дві сторони таблиці, при чотирьох- і п'ятичленному вирівнюванні - відповідно три і чотири рядки. Якщо число даних не правильне, то таке скорочення даних навряд чи буде доцільним.

Питання про доцільну довжину часового ряду дуже складне. З одного боку, як і завжди при пошуку апроксимуючої формули або рівняння регресії, виникає природне прагнення до збільшення масиву спостережень з метою підвищення точності надійності результатів, з другого боку, при обробці часових рядів слід враховувати небажаність використання старих даних. Приймати ці суперечливі вимоги можна тільки за рахунок зменшення довжини інтервалів часового ряду – скорочуючи крок ряду (шляхом переходу, наприклад від квартальних даних до місячних, від місячних до тижневих і т.п., якщо такі дані за матеріалами звітності можна мати).

Приклад. Дані собівартості пасажироперевезень міським електричним транспортом, поданих в табл. 12.4, вирівняти за ковзною середньою і побудувати графік.

Вирішення

Статистичні дані собівартості пасажироперевезень по депо й розрахунок ковзних наведено в табл. 12.4.

Таблиця 12.4 - Статистичні дані про собівартість пасажироперевезень по депо

t	Собівартість С, коп.	Трич-лен- ні суми	Тричлен- ні ковзні середні	Чотири-член- ні суми	Чотири-членні ковзні середні	П’яті-член- ні суми	П’яти-член- ні ковзні середні
	65,9	-	-	-	-	-	-
	66,9	201,3	67,3	269,4	67,3	-	-
	69,1	203,5	67,8	271,7	67,9	338,2	67,6
	67,5	204,8	68,2	274,7	68,6	339,3	6,8
	68,2	205,6	68,5	276,5	69,1	345,6	69,1
	69,9	209,0	69,5	281,8	70,4	349,3	69,7
	70,9	213,6	71,2	285,7	71,4	358,5	71,7
	72,8	215,8	71,9	288,5	72,1	361,4	72,2
	72,1	217,7	72,5	290,5	72,6	363,7	72,7
	72,8	217,7	72,5	290,9	72,7	365,7	72,9
	72,8	278,8	72,9	-	-	-	-
	73,1	-	-	-	-	-	-

Як бачимо, середні дані більш наочно виражають основну тенденцію собівартості перевезення пасажирів. Вихідні дані, що різно ковзають, подані на рис. 12.1.

Рис. 12.1 - Вихідні дані, ковзні й вирівнююча парабола:

1- вихідні дані; 2- тричленні ковзні; 3- чотиричленні ковзні; 4- п’ятичленні середні; 5- вирівнююча парабола.

При визначенні загальної тенденції виникають два завдання: вибір форми рівняння, тобто вид функції d(t); обчислення параметрів рівняння.

Слід зазначити, що аналіз часових рядів спрямований не тільки на визначення загальної тенденції і побудову моделі динаміки, а й на прогнозування економічних показників.

При виборі форми рівняння необхідно, як у статистичному регресійному аналізі, добре знати процес за суттю. Так, для короткострокового прогнозування багатих механіко– економічних показників найкращою формою тренда є показова, що описує зростання за законом складних процесів, для більш тривалого періоду прогнозування по цілому ряду показників - експонента з насиченням. Якщо ж сутність процесу не вимагає певної форми управління, то вибір проводять за якнайменшою залишковою дисперсією. Графічна ілюстрація часового ряду також допоможе в цьому виборі.

Практика показує, що доцільно піддавати випробуванню залишкову дисперсію по чотирьох монотонних функціях:

1. Лінійна

;

2. Степенева

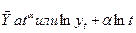
3. Експоненціальна

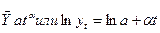
4. Експоненти з насиченням

При цьому відхилення від тренду визначаються відповідно у вигляді:

(12.1)

Всі параметри α знаходять за методом якнайменших квадратів, що приводить до системи нормальних рівнянь:

(12.2)

(12.3)

(12.4)

(12.5)

Знайшовши для відповідної залежності, знаходять функцію, яка в порівнянні з іншими найкраще апроксимує початковий часовий ряд.

Використання з метою апроксимації багатопараметричних функцій недоцільне. Хоч за допомогою таких функцій можна отримати добре наближення вихідних даних, але, таким чином математично описується не стільки загальна тенденція, скільки випадкові від неї відхилення; з'являються невиправдані особливості процесу - максимуми і мінімуми. Крім того, складання таких функцій і їх застосування для практичних розрахунків різко ускладнюється.

Приклад. Для вищеперерахованих даних, використовуючи степеневу залежність , розраховуємо її параметри.

Вирішення

Для визначення параметрів рівняння розрахунки подано в табл. 12.5.

Таблиця 12.5 - Розрахунок статистичних характеристик рівняння.

	Yt	ln t	ln t2	ln Yt	ln Yt ln t		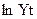Yt	ε	ε2
	65,9	0,00	0,00	1,8189	0,00	1,8035	63,6	2,3	5,29
	66,9	0,3010	0,0906	1,8254	0,5494	1,8211	66,24	0,66	0,44
	69,1	0,4771	0,2276	1,8395	0,8774	1,8314	67,32	1,28	1,64
	67,5	0,6021	0,3625	1,8293	1,1014	1,8387	68,98	-1,48	2,19
	68,2	0,6990	0,4886	1,8331	1,2813	1,8443	69,88	-1,68	2,82
	69,9	0,7782	0,6056	1,8445	1,4354	1,8490	70,13	0,73	0,53
	70,9	0,8451	0,7142	1,8505	1,5639	1,8524	71,19	-0,29	0,08
	72,9	0,9031	0,8156	1,8627	1,6822	1,8566	71,88	1,02	1,04
	72,1	0,9542	0,9109	1,8579	1,7728	1,8593	72,33	-0,23	0,05
	72,8	1,000	1,00	1,8621	1,8626	1,8620	72,88	-0,08	0,00
	72,8	1,0414	1,0845	1,8621	1,9392	1,8644	73,16	-0,36	0,13
	73,2	1,0792	1,1647	1,8645	2,0122	1,8666	73,52	-0,32	0,12
∑		8,6824	7,4648	22,1506	16,0959				14,32

Система нормальних рівнянь має вигляд

(12.6)

Підставивши відповідні значення з табл. 12.5, отримаємо

(12.7)

Вирішивши систему рівнянь, одержимо:

α=0,0585, lna=1,8035.

Маємо рівняння:

(12.8)

Прогноз на 13 і 14 періоди складе: Y₁₃=72,83; Y_m=73,02.

Середній квартал відхилення вихідних значень від розрахункових (дисперсія)

(12.9)

а середні квадратичні відхилення що в порівнянні з середнім розміром складає

Зазначимо, що похибки апроксимації особливо великі на кінцях базисного періоду, що обумовлюють велику помилку прогнозу. Можна сказати, що залежність підібрана невдало.

Якщо протягом базисного періоду досліджений процес суттєво змінився в результаті появи нових чинників (сезонні коливання), то для апроксимації часового ряду слід скористатися двома або більше окремими аналітичними виразами, розглядаючи їх як частини науково – безперервної функції. При цьому прогнозування проводиться за останньою дугою і необхідно уточнити, який допустимий інтервал прогнозування. Факт істотності змін для показника слід встановлювати як якісно, так і статистично.

Можна скористатися і графічним способом: побудувавши три тренди по кожному періоду в цілому по всьому ряду, порівняти графічно, на скільки близько загальний тренд огинає обидва часткових.

Статистична перевірка може бути здійснена наступним прикладом дисперсійного аналізу. Нехай значення показника до і після деякого моменту задані рядами:

_{11, 12}... _1h1; (12.10)

_{21, 22}... _2h1. (12.11)

з середніми значеннями і дисперсіями, визначуваними за формулами

; (12.12)

Обчислюємо загальну середня і загальну дисперсію з'єднаного ряду

; . (12.13)

Розчленувавши повну дисперсію ряду на частини, одержуємо

. (12.14)

Враховуючи число ступенів свободи кожної з сум в рівнянні, визначаємо

; . (12.15)

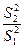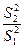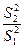Відношення порівнюємо з відповідним значенням розподілу Фішера. Якщо < F(5%) [1, n-2] при рівні значущості 5% вважаємо періоди, що вивчаються, неістотно різними у значенні даного показника . Якщо < F_5% [ 1, n-2 ] при рівні значущості 1% вважаємо періоди, що вивчаються, суттєво різними за показником і будуємо тренд з двох частин, різних тільки за параметрами або видом функції d(t).

Приклад. Методику обробки рядів динаміки за наявності сезонних коливань можна проілюструвати на прикладі собівартості пасажироперевезень одним з тролейбусних рівнянь за період 2002-2007 рр.

Вирішення

Виявлення загальної тенденції на підставі даних табл. 12.6 починаємо з побудови графіка.

Таблиця 12.6 - Динаміка статистичних показників

Роки	t	Значення показника, С, коп.	Квартал
I	II	III	IV
		58,71	62,3	56,88	59,34	56,72
		60,13	62,78	58,35	60,84	58,78
		60,83	63,47	57,88	62,58	59,4
		65,70	69,52	63,02	63,89	66,51
		66,08	67,23	62,99	65,65	67,54
		66,76	68,59	60,56	66,00	68,29

Рис. 12.2 - Динаміка собівартості пасажироперевезень

У цьому прикладі (рис. 12.2) спостерігається різкий перелом характеру змін в 2004 р. Тому неможливо підібрати єдину математичну функцію зростання, задовільно апроксимуючу дані про собівартість пасажироперевезень за всі роки. У зв'язку з цим розбиваємо тимчасовий діапазон на дві частини - 2002-2005 рр. і 2005-2007 рр. Для першого ряду підбираємо експоненту, для другого - експоненту з насиченням. При визначенні параметрів рівнянь використовуємо розрахунки, зведені відповідно в табл. 12.7, 12.8.

Таблиця 12.7 - Розрахунок параметрів експоненти

Ро- ки	Y	ℓny	t	V= ℓny-1,78	Vt	t2		ℓny=1,78+		ε	ε2	β%
	58,71	1,7761		-0,0039			-0,013	1,7787	60,08	-1,37	1,88	2,28
	60,13	1,7791		-0,0004	-0,004		0,0021	1,7821	60,53	-0,4	0,16	0,66
	60,83	1,7841		0,0041	0,0082		0,0155	1,7955	62,44	-1,61	2,59	2,57
	65,70	1,8176		0,0376	0,1182		0,0289	1,8089	64,40	1,3	1,69	2,01
∑	х	х		0,0374	0,1206		х	х	х	х	6,32	х

Таблиця 12.8 - Розрахунок параметрів експоненти з насиченням

Роки	Y	ℓny	t	t1=t-2	V= ℓny-1,82					ℓny= 1,82+		ε	ε 2	β%
	65,7	1,8176			-0,0024		-0,024		-0,0084	1,8116	64,8	0,9	0,81	1,388
	65,08	1,82			0,000	0,50	0,00	0,250	0,0033	1,8233	66,58	-0,5	0,25	0,75
	66,76	1,8245			0,0045	0,333	0,0015	0,111	0,0072	1,8272	67,16	-0,4	0,16	0,59
∑	х	х	х	х	0,0021	1,833	-0,0009	1,361	х	х	х	х	1,22	х

Системи нормальних рівнянь має наступний вигляд:

; . (12.16)

Звідки

ℓ_na =-0,0113, a= 0,0134; ℓ_na¹ =0,015, а¹= -0,0234;

V = -0,0113+0,0134 t; V¹=0,015 - .

Тоді одержуємо

ℓ_{n t} = 1,7687 + 0,0134 t; ℓ_{n t} = 1,835 - ;

=58,7^{0,0134 t} 0 ≤ t ≤ 3; _t 3≤ t ≤ 5

max β% = 2,58; max β% = 1,388.

Апроксимація цілком задовільна.

Для 2005 р. приймаємо значення собівартості

= 64,60.

Прогноз на 2004 р. При t=6

ℓ_nу = 1,835 - = 1,829, = 67,49.

Проте через сезонні коливання прогнозування за сумарними річними даними є абсолютно недостатнім. Тому необхідно прогнозувати за окремими періодами, в даному прикладі за вихідними квартальними даними.