Теорема Гаусса

Задать электрическое поле – это значит указать в каждой точке величину и направление вектора напряженности (рисунок 5).

Для большей наглядности при графическом изображении электростатических полей используют линии вектра напряженности, которые проводятся так, чтобы вектора были касательными к ним в каждой точке (рисунок 6).

Для полей точечных зарядов линии вектора имеют вид радиальных прямых, начинающихся или заканчивающихся на зарядах – источниках полей (рисунок 7).

В случае, если силовые линии параллельны друг другу и расположены на равных расстояниях, поле называют однородным (рисунок 8). Густота линий в данной части поля характеризует величину вектора . Для большей наглядности условились выбирать густоту линий вектора так, чтобы через единицу площади поверхности, перпендикулярной вектору , проходило число линий, равное величине (рисунок 9): S = 1 м², Е = 5 единиц.

При расчете электростатических полей часто используют понятие потока вектора напряженности электростатического поля.

Потоком Ф_Е вектора напряженности через произвольную поверхность называют число силовых линий, пересекающих данную поверхность.

Рассчитаем поток Ф_Е однородного поля через площадку величиной S, единичный вектор нормали к которой составляет произвольный угол a с вектором (рисунок 10).

Рисунок 9

Разложим вектор на 2 компонента: и . Из рисунка видно, что вектор «скользит» по площадке, не пересекая ее и, следовательно, не формирует поток. С потоком связана нормальная составляющая . Так как по условию густота линий вектор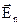а равна , то количество линий, пересекающих площадку S (поток Ф_Е), определяется формулой

, (7)

где E_n – проекция вектора на нормаль к площадке.

Если ввести в рассмотрение вектор , имеющий величину и направленный так же, как и вектор , то равенство (7) можно записать в векторном виде

.

Если поле неоднородно или поверхность имеет произвольную форму, то для расчета потока Ф_Е поверхность S разбивают на столь малые площадки dS, чтобы в их пределах поле могло быть однородным, и находят элементарный поток через площадку , а затем полный поток рассматривают как интеграл

.

Поток вектора непосредственно связан с величиной зарядов – источников поля.

Пусть имеется поле точечного заряда ₊Q. Подсчитаем поток вектора через произвольную сферическую поверхность S, в центре которой находится точечный заряд (рисунок 11). Так векторы в каждой точке перпендикулярны к поверхности сферы и распределены равномерно, то

Q

.

	Если бы поверхность была не сферическая, а произвольная, то результат был бы тот

же, так как число линий не изменится. Если поле создается группой зарядов Q_!, Q_2, Q₃, то полный поток через замкнутую поверхность с учетом знаков будет равен сумме зарядов, деленной на ee₀

.

Приведенные рассуждения являются содержанием теоремы Гаусса:

поток вектора напряженности через произвольную замкнутую поверхность равен алгебраической сумме зарядов, которые она охватывает, деленной на ee₀

. (8)

Если внутри поверхности зарядов нет, то

,

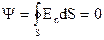так как число линий , входящих и выходящих из поверхности, равны.

При рассмотрении полей, создаваемых непрерывно распределенными по объему тела зарядами, величину заряда в теореме Гаусса выражают через объемную плотность заряда r, равную отношению заряда dQ к бесконечно малому объему dV, в котором заключен этот заряд

.

Зная плотность заряда в каждой точке пространства, можно найти суммарный заряд, заключенный внутри замкнутой поверхности S. Для этого нужно вычислить интеграл от rdV по объему, ограниченному поверхностью S

.

Таким образом, формуле (8) можно придать вид

Рассчитать электрическое поле – значит найти значение вектора напряженности в каждой точке поля по известному распределению зарядов или описать распределение зарядов по заданным значениям напряженности.

В зависимости от формы заряженных тел, создающих поле, используют три метода расчета полей:

1) на основе принципа суперпозиции полей;

2) на основе теоремы Гаусса;

3) на основе связи между напряженностью и потенциалом.

Метод расчета, основанный на применении принципа суперпозиции полей, используется при расчете поля, создаваемого совокупностью точечных зарядов. С помощью этого метода мы рассчитывали поле диполя.

Метод, основанный на использовании теоремы Гаусса, применяется для расчета полей, создаваемых заряженными телами правильной формы, и используется по следующей схеме: рассчитывается поток вектора (Q – известно), причем произвольная замкнутая поверхность выбирается так, чтобы в каждой ее точке и , то есть cosa = 1,

E_n= E, тогда

где S – площадь поверхности, которая может быть вычислена из геометрических соображений.

Пример 1. Рассчитать поле заряженной сферы радиуса R. Заряд равномерно распределен по поверхности (рисунок 12).

Задача распадается на две: 1) найти поле вне сферы; 2) найти поле внутри сферы.

Найдем в произвольной точке на расстоянии r₁> R от центра. Для этого выберем произвольную поверхность, охватывающую сферу, и рассчитаем поток вектора r₁ через нее . Но по теореме Гаусса откуда .

Как видим, поле вне заряженной сферы определяется как поле точечного заряда Q, помещенного в центр сферы.

Выбирая произвольную точку r внутри сферы и определяя поток Y через сферу радиуса r

убеждаемся, что поле внутри сферы отсутствует, так как нет зарядов Q внутри выбранной поверхности.

Пример 2. Рассчитать поле бесконечной заряженной плоскости с равномерно распределенной поверхностной плотностью заряда (рисунок 13).

Так как поле однородное, следовательно? в любой точке E = const. В качестве произвольной поверхности выберем цилиндр радиуса r, основания которого параллельны поверхности, и рассчитаем поток вектора через поверхность цилиндра. Поток вектора через боковую поверхность равен нулю, а через основания .

По теореме Гаусса

Откуда 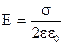. (9)

Направление определяется знаком s. При s > 0 линии идут от плоскости, при s < 0 они идут к плоскости.

Из формулы (9) следует, что напряженность поля не зависит от положения точки, в которой она рассчитывается, то есть во всех точках напряженность имеет одинаковую величину и направление. Такое поле называется однородным. Линии однородного поля параллельны и имеют одинаковую густоту.

Используя полученный в примере 2 результат, легко рассчитать поле двух разноименно заряженных бесконечных плоскостей (конденсатора) (рисунок 14).

Как видно из рисунка 14 поле вне конденсатора равно нулю, а внутри

Поученный результат справедлив и для пластин конечных размеров, если размеры пластин много больше расстояния между ними.

Таким образом, успех применения теоремы Гаусса для расчета полей зависит от удачного выбора произвольной поверхности для вычисления потока вектора .

Из законов, описывающих электростатическое поле, вытекают некоторые из его свойств. Электростатическое поле является центральным, то есть оно имеет источник (центр) и свойства его одинаковы во всех направлениях. Это подтверждается, в частности, теоремой Гаусса. Силовые линии поля не пересекаются и в этом плане электростатическое поле похоже на гравитационное.

Вектор напряжённости является силовой характеристикой электрического поля. С энергетической точки зрения электрическое поле характеризуется потенциалом в каждой точке (или разностью потенциалов двух точек).

Электрическая энергия – это самый универсальный вид энергии, который может быть превращён в любой другой вид. Поэтому изучение энергетической характеристики электрического поля приобретает особое значение.

Потенциал и вектор напряжённости в каждой точке поля связаны между собой, поэтому по изменению потенциала в каждой точке можно судить о силовых характеристиках электрического поля, то есть рассчитывать электрическое поле.

3 Циркуляция вектора напряжённости

Заряд, помещённый в электростатическое поле, перемещается под действием кулоновских сил. Действие этих сил в каждой точке характеризуется величиной вектора напряжённости .

Так как при взаимодействии зарядов происходит превращение одной формы движения материи в другую (электрической в механическую), то естественно этот процесс следует характеризовать величиной работы силы Кулона. При перемещении заряда из точки поля I в точку 2 совершается работа, которую можно вычислить следующим образом.

Рисунок 15

Разобьём путь 1-2 (рисунок 15) на элементы :

Тогда полная работа на пути 1-2 будет равна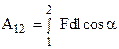

Заменяя , получим . (10)

Таким образом, работа перемещения заряда зависит от характера поля и величины движущегося заряда , перемещения/ Как видно из выражения (10), отношение работы перемещения заряда из одной точки поля в другую к величине этого заряда

определяется лишь характером поля и положением точек 1 и 2.

Эта величина называется разностью потенциалов двух точек и обозначается так:

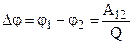. (11)

В качестве примера рассмотрим поле точечного заряда (рисунок 16). Так как в этом случае

, то из формулы (10) получим .

Рисунок 16

Учитывая, что , получим . (11)

Анализ полученного выражения позволяет сделать два очень важных заключения:

1) известно, что работа может быть вычислена как изменение энергии системы. Следовательно, каждое из слагаемых в формуле (12) представляет собой выражение энергии взаимодействия точечных зарядов и в различных точках:

, . (12)

Так как величина энергии в этом случае зависит лишь от взаимного расположения зарядов и и от типа взаимодействия (от характера сил), то это потенциальная энергия.

2) Из выражения (12) видно, что работа перемещения заряда в электростатическом поле не зависит от пути перемещения и, следовательно, работа по замкнутому контуру равна нулю. Это справедливо не только для полей точечных зарядов, но и для электростатических полей зарядов любой формы. Выражение (10) в этом случае имеет вид