Построение прямой, проходящей через две заданные точки

Даны две точки A (x1, y1) и B(x2, y2). Задано x1=-1, y1=-1, x2=1, y2=1. Через эти точки надо провести прямую линию и найти расстояние между ними.

Уравнение прямой может быть записано так:

Угловой коэффициент определяется формулой:

Уравнение можно записать:

Расстояние между двумя точками вычисляется по формуле:

На рис.8.27 приведено решение этой задачи в системе Mathcad. Обратите внимание на форматирование графика и использование текстового блока для того, чтобы пометить точку A и B.

Рисунок 8.27 - График прямой, проходящей через две заданные точки

8.5.2 Построение графика функции y = f(x), графика первой и второй производной этой функции

Найти производную первого и второго порядка функции y = f(x) и на одном графике построить график функции y = f(x), график первой и второй производной этой функции. Решение этой задачи приведено на рис.8.28.

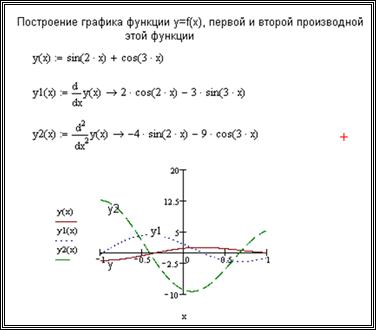
Рисунок 8.28 - График функции y = f(x), первой и второй производной этой функции

8.5.3. Построение графика касательной и нормали к кривой y = f(x)

Надо построить график касательной и нормали к кривой y = f(x) в точке с абсциссой a. Для этого необходимо найти первую производную функции y = f(x).

Если функция y = f(x) в точке a имеет конечную производную, то уравнение касательной имеет вид:

.

Если f’(a) = ¥, то уравнение касательной имеет вид: x = a.

Если f’(a) ¹ 0, то уравнение нормали имеет вид:

.

Если f’(a) = 0, то уравнение нормали имеет вид: x = a.

Пример решения данной задачи приведен на рис.8.29. Для правильного представления нормали масштабы по осям должны быть равны.

Рисунок 8.29 - График касательной и нормали к кривой в заданной точке