Способы образования выборочной совокупности

Собственно случайный отбор – отбор в совершенно случайном порядке (жеребьевка).

Может быть осуществлен в двух видах:

ü повторный отбор – отобранная для наблюдения единица регистрируется и возвращается в исходную совокупность, таким образом, возникает возможность отобрать для наблюдения данную единицу еще раз. Вероятность отбора у всех единиц одинакова.

ü бесповторный отбор – отобранная для наблюдения едини­ца регистрируется и не возвращается в исходную совокупность. Та­ким образом, единица для наблюдения может быть отобрана только один раз, а вероятность отбора последующих единиц увеличивается.

Механический отбор – отбор единиц в выборочную совокуп­ность производится из генеральной совокупности через равные ин­тервалы (так сказать, механическим путем). При этом все единицы генеральной совокупности должны быть упорядочены по какому-либо признаку: существенному, второстепенному или нейтральному. Далее, генеральная совокупность делится на столько групп, сколько единиц необходимо отобрать в выборочную совокупность. В первой группе случайным образом отбирается первая единица для наблюдения. А затем во всех последующих группах отбираются единицы с этим же порядковым номером. Таким образом, механическая выбор­ка по принципу своей организации бывает только бесповторной.

Типический отбор – генеральная совокупность предваритель­но разбивается на однородные по какому-либо признаку (типу) груп­пы. Далее, из каждой группы отбираются единицы в вы­борочную совокупность либо в собственно случайном порядке (повторно или бесповторно), либо механически.

Отбор в группах осуществляется независимо, т. е. каждая груп­па рассматривается как отдельная совокупность. Общим соблюдает­ся лишь способ отбора. Данный способ применяется при изучении сложных явлений, например, при исследовании производительности труда работников, разбитых на группы по квалификации. Отбор единиц в выборочную совокупность может проводиться повторным и бесповторным способом.

Серийный (гнездовой) отбор – генеральная совокупность разбивается на серии (гнезда) и для наблюдения отбираются не отдель­ные единицы, а целые серии (гнёзда), внутри которых единицы обследуются сплошным способом (например, товар упакован в короб­ки, т. е. серия – коробка). Отбор серий производится либо в собствен­но случай­ном, либо в механическом порядке.

На практике эти способы обычно применяются не в «чистом» виде, а комбинируются в различных сочетаниях (например, серийный отбор со случайной выборкой), так как отбор единиц из генеральной совокупности в действительности – сложный процесс.

8.2. Генеральная и выборочная совокупность,
их обобщающие характеристики.
Репрезентативность выборки

Итак, генеральная совокупность – это, с одной стороны, исходная совокупность, из которой производится отбор единиц для наблюдения, а с другой – совокупность, свойства которой стремятся определить по результатам выборочного наблюдения.

Выборочная совокупность – та часть единиц совокупности, которая отбирается для статистического наблюдения.

Основная задача выборочного наблюдения – получить представление о показателях генеральной совокупности на основе изучения выборочной совокупности.

В выборочном наблюдении применяются 2 обобщающих показателя:

ü среднее значение признака,

ü доля альтернативного признака.

Среднее значение признака – это обобщающая характеристика изучаемой совокупности по количественно варьирующему признаку (например, средняя заработная плата одного работника).

Доля альтернативного признака дает характеристику совокуп­ности по альтернативно варьирующему признаку и исчисляется как отношение количества единиц совокупности, обладающих интересующим значением признака, к общему количеству единиц совокупности (относительная величина структуры). Например, при обследовании студентов определяется доля студентов, получающих стипендию.

Альтернативно варьирующий признак – это признак, имеющий всего два значения: да, нет (например, пол: мужской, женский). Любую множественную вариацию можно свести к альтернативной: интересует значение признака или нет.

В генеральной совокупности среднее значение признака будем называть генеральной средней (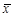), а долю единиц, обладающих интересующим значением признака, – генеральной долей (p).

В выборочной совокупности среднее значение признака будем называть выборочной средней (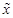), а долю единиц, обладающих интересующим значением признака, – выборочной долей ().

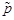Задача выборочного наблюдения – получить достоверное пред­ставление о генеральных показателях доли и средней на основе аналогичных характеристик выборочной совокупности. А так как единицы в выборочную совокупность отбираются в случайном порядке, то между выборочными и генеральными показателями всегда существуют расхождения – ошибки выборки или ошибки репрезентативности. Математически это можно выразить следующим образом:

ü для средней –

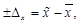(1)

ü для доли –

(2)

8.3. Средняя и предельная ошибки
выборочной средней и выборочной доли

Ошибка выборки (ошибка репрезентативности) зависит от численности выборки и от степени варьирования изучаемого признака. Все возможные расхождения между характеристиками выборочной и генеральной совокупности аккумулируются в формуле средней ошибки выборки. Она рассчитывается по-разному в зависимости от способа отбора: повторный или бесповторный.

– Средняя ошибка выборки (m – мю) при повторном отборе.

ü для средней –

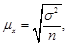(3)

где n – количество единиц выборочной совокупности, – диспер­сия варьирующего признака в выборочной совокупности:

· в форме простой для индивидуальных данных

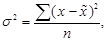(4)

· в форме взвешенной для сгруппированных данных

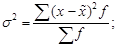(5)

ü для доли –

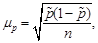(6)

где 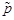– доля интересующего значения признака в выборочной совокупности:

(7)

и n_да – количество единиц в выборочной совокупности, обладающих интересующим признаком, n – общее количество единиц в выборочной совокупности, 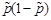– дисперсия альтернативного признака.

– Средняя ошибка выборки при бесповторном отборе.

При этом способе отбора количество единиц генеральной совокупности сокра­щается в процессе выборки и вероятность отбора каждой последующей единицы увеличивается, что математически отображается в выражении

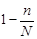(), (8)

где N – количество единиц в генеральной совокупности.

Поэтому средняя ошибка выборки при бесповторном отборе

ü для средней –

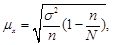(9)

ü для доли –

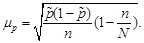(10)

Приведённые формулы (3), (6), (9), (10) позволяют определить среднюю величину отклонений характеристик генеральной совокупности от выборочных характеристик, равную 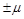. Например, по выборочным данным средний срок горения лампочек составляет 3000 часов, а 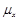= 50 часов. Следовательно, во всей партии лампочки будут гореть (3000 ± 50) часов, т. е. от 2950 до 3050 часов.

Доказано, что генеральные характеристики отклоняются от выборочных на величину ±μ с вероятностью, равной 0,638. Это оз­начает, что в 683 случаях из 1000 генеральная характеристика будет находиться в пределах ±μ от выборочной характеристики, а в 317 случаях выйдет за эти пределы.

Вероятность суждений можно изменить и, следовательно, из­менить границы характеристик генеральной совокупности, если скор­ректировать среднюю ошибку выборки на коэффициент доверия (t), который зависит от вероятности, с которой можно гарантировать, что предельная ошибка не превысит t -кратную среднюю ошибку. Данный показатель находится по готовым таблицам функции F(t), определённой русским математиком А.М. Ляпуновым применитель­но к нормальному распределению.

Величина, полученная как произведение коэффициента доверия и средней ошибки выборки, называется предельной ошибкой выборки (D – дельта)

ü для средней:

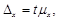(11)

ü для доли:

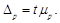(12)

8.4. Определение необходимой
численности выборки

Размер ошибки выборки прежде всего зависит от количества единиц в выборочной совокупности (численности выборки). Средняя ошибка выборки обратно пропорциональна 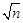, т. е. при увеличении численности выборки в 4 раза её ошибки уменьшаются вдвое.

Увеличивая количество единиц в выборочной совокупности, можно довести её ошибку до очень малых размеров, однако надо помнить, что задача выборочного наблюдения – получение необходимой информации с минимальными затратами. Следователь­но, надо находить в каждом случае оптимальную численность выборки. Определение необходимой численности выборки основывается на формуле предельной ошибки выборки.

При повторном отборе:

ü для средней предельная ошибка выборки рассчитывается по формуле

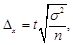(13)

тогда необходимая численность выборки

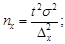(14)

ü для доли предельная ошибка выборки рассчитывается по формуле

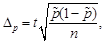(15)

тогда необходимая численность выборки

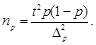(16)

При бесповторном отборе:

ü для средней предельная ошибка выборки рассчитывается по формуле

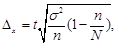(17)

тогда необходимая численность выборки

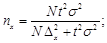(18)

ü для доли предельная ошибка выборки рассчитывается по формуле

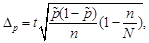(19)

тогда необходимая численность выборки

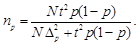(20)

Примечание: для определения необходимой численности вы­борки при исследовании конкретного явления в указанных формулах применяют генеральную дисперсию и генеральную долю, т. е. используют показатели, рассчитанные при изучении исходной совокупности.