Основное уравнение кинетической теории газов

Если в предыдущем разделе применялся термодинамический метод исследования, то в этом разделе будет использован статистический метод исследования молекулярных процессов. На основании исследования совокупного действия молекул будут получены такие термодинамические параметры, как давление и температура.

Для расчетов воспользуемся моделью идеального газа с точки зрения молекулярно-кинетической теории:

1. молекулы газа непрерывно и хаотично движутся;

2. молекулы взаимодействуют только во время удара;

3. удары молекул абсолютно упругие;

4. размеры молекул малы по сравнению с расстоянием между ними.

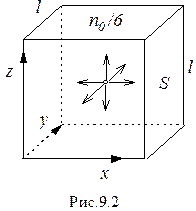Пусть в сосуде кубической формы объемом V = l ³, где l - длина ребра (рис. 9.2), число молекул в единице объема равно n_o. Молекулы движутся хаотично и, соударяясь со стенкой площадью S = l ², оказывают на нее давление. Результаты расчета давления на стенку не изменятся, если хаотическое движение молекул заменить направленным движением их вдоль осей x, y, z. Тогда со стенкой S будет соударяться третья часть от всех молекул, равная

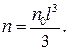(9.8)

При каждом соударении со стенкой молекула передает ей импульс, равный mv₁ - (- mv₁) = 2 mv₁, где m - масса молекулы, v₁ -ее скорость. За время Dt молекула пройдет путь v₁Dt, соударится со стенкой число раз, равное v₁Dt/2l, и передаст стенке импульс DP₁ = mv₁²Dt/l. Просуммируем импульс, переданный стенке всеми n молекулами: DP = (mDt/l)(v₁² + v₂² +...+ v_n²). В данном выражении находится сумма квадратов скоростей. Статистическое усреднение будет заключаться в том, что мы введем новую среднюю величину - среднеквадратичную скорость - по формуле v _кв ² = (v₁² + v₂² +...+ v_n²)/n. Следует заметить, что v _кв приблизительно на 10% больше, чем средняя скорость молекулы, которая определяется по формуле: v _ср = (v₁ + v₂ +... + v_n)/n. Используя выражение для v _кв ², получим DP = mv _кв ²Dtn/l. По второму закону Ньютона на стенку будет действовать сила F = DP/Dt = mv _кв ²n/l. Давление газа на стенку найдем по формуле p = F/S = F/l ² или p = mv _кв² n/l³. Используя формулу (9.8), получим окончательно

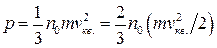(9.9)

Мы получили основное уравнение кинетической теории газов, которое связывает макроскопический параметр - давление газа - с микроскопическими параметрами молекул. Величина n_o(mv _кв ²/2) есть кинетическая энергия молекул, заключенная в единице объема. Отсюда следует, что давление есть мера плотности кинетической энергии молекул.

Сравнивая формулы (9.9) и (9.7), получим выражение для средней кинетической энергии молекулы

(9.10)