Работа и энергия

Пусть тело, на которое действует сила , проходит, двигаясь по некоторой траектории путь S. При этом сила либо изменяет скорость тела, сообщая ему ускорение, либо компенсирует действие другой силы (или сил), противодействующих движению. Для характеристики действия силы, в результате которого совершается перемещение тела, используется величина, называемая работой.

ОПРЕДЕЛЕНИЕ: Работой называется скалярная величина, численно равная произведению действующей силы (F_S) на направление перемещения и величины пути (S), проходимого точкой приложения силы A=F_S×S.

Это выражение справедливо, если величина проекции силы F_S=const. В частности, это имеет место, когда тело движется прямолинейно и постоянная по величине сила F образует с направлением движения постоянный угол a (рис. 3.2). Т.к. F_S=F· cos a, то A=F·S· cos a.

Работа алгебраическая величина. Если

1. , то cos a > 0 Þ A > 0;

2. , то A<0, т.к. cos a < 0;

3. 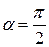, то cos a = 0 Þ A = 0.

Последнее обстоятельство особенно отчетливо показывает, что понятие работы в механике существенно отличается от обыденного представления о работе.

Пример: Чтобы держать тяжелый груз, а тем более нести его по горизонтальному пути, носильщик затрачивает много усилий, хотя якобы «не совершает работу». Работа как механическая величина в этих случаях не равна нулю, так как эта работа складывается из множества перемещений вниз и вверх. Причем при перемещении вниз уменьшение потенциальной энергии в поле тяжести не переходит в полезную работу.

Если величина проекции силы на направление перемещения не постоянная величина во время движения, то для вычисления работы необходимо путь S разбить на элементарные участки DS, взяв их настолько малыми, что за время прохождения телом такого участка величину F_S можно было считать практически неизменной (рис. 3.3).

Тогда для элементарного участка пути: DA @ F_S×DS.

А работа на всем пути S будет вычисляться как сумма элементарных работ: .

При ×DS _i ® 0 получим строгое равенство:

График F_S как функции положения точки на траектории представлен на рис. 3.3. Видно, что элементарная работа равна площади заштрихованной полоски, а работа A на пути от точки 1 до точки 2 численно равна площади фигуры, ограниченной кривой F_S, вертикальными прямыми 1 и 2 и осью S.

Воспользовавшись скалярным произведением векторов, выражение для работы можно записать в виде:

, (3.6)

где под подразумевается вектор элементарного перемещения. Если сила имеет постоянную величину и направление, то вектор в последнем выражении можно вынести за знак интеграла, в результате чего выражение для работы примет вид:

, (3.7)

где – вектор перемещения, а S_F – его проекция на направление силы.

В системе СИ единицей работы является 1Дж, который равен работе, совершаемой силой в 1Н на пути в 1м. 1Дж=1Н×1м.