Определение расстояний, недоступных для измерения мерной лентой

Если непосредственное измерение линии на местности по каким-либо причинам невозможно, то применяют различные косвенные способы определения расстояний. Наиболее часто в практике линейных измерений для решения этой задачи используют метод прямой засечки. Для определения длины линии S необходимо, как видно из рис.52, измерить на местности горизонтальное проложение базиса в (дважды, в прямом и обратном направлениях) и прилегающие к нему углы α и β. Тогда искомая сторона S определится по теореме синусов:

S = в sinβ/sin(α+β).

Для контроля измерений и вычислений рекомендуется разбить еще один базис в ₁ и после измерений углов α₁ и β₁ вычислить контрольное значение S ₁.

Рис. 52. Определение недоступного расстояния

Если есть возможность, то рекомендуется для контроля измерений углов в треугольниках измерить также и углы γ и γ₁, что позволит определить угловую невязку и оценить надежность угловых измерений. .

Если относительная погрешность

,

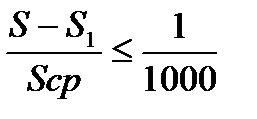где 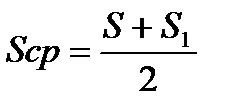, то среднее

из двух измерений принимается за окончательное значение определяемой линии. Желательно, чтобы каждый из базисов был не менее 0,6 длины определяемой линии, а горизонтальные углы не выходили за пределы 30−150°.

В некоторых случаях для определения длины линии строят на местности два равных друг другу прямоугольных треугольника с взаимно параллельными сторонами, причем в качестве стороны одного из них берут недоступный для измерения отрезок. Как видно из рис. 52, длина недоступной линии AB равна длине линии A'B', которую уже можно измерить непосредственно мерной лентой в прямом и обратном направлениях и получить величину недоступного расстояния.