Определение высоты сооружения

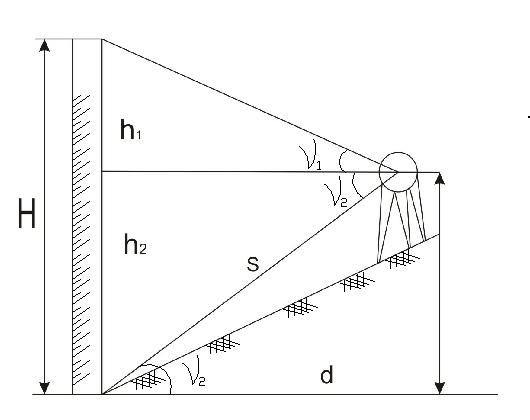
Для определения высоты сооружения на некотором удалении от сооружения устанавливают теодолит и расстояние S от центра теодолита до центра сооружения измеряют непосредственно на местности при помощи стальной мерной ленты. Затем, используя вертикальный круг теодолита, согласно рис. 47, измеряют вертикальные углы ν₁ ν₂ и угол наклона линии местности S к горизонту. Высота сооружения определяется выражением

H = h ₁+ h ₂,

если место установки теодолита выше основания сооружения, как на рис. 47, а и

H = h ₁− h ₂.

если место установки теодолита ниже основания сооружения (рис.47, б), где h ₁ = d tgν₁; h ₂ = d tgν₂; d = S cosν_2.

а б

Рис.48. Схема определения высоты сооружения

Расстояние S и высоту Н сооружения определяют для контроля дважды и находят среднее

.

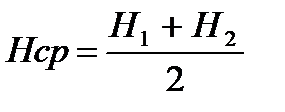Если относительная погрешность

то Н _ср принимают за окончательный результат определения высоты сооружения.

Однако на практике не всегда имеется возможность непосредственно на местности измерить расстояние от центра инструмента до центра сооружения. В этом случае, как показано на рис. 48, в стороне от сооружения в удобном месте разбивают базис в, измеряя его стальной лентой дважды в прямом и обратном направлениях.

Устанавливая теодолит последовательно в точках А и В, измеряют вертикальные ν₁, ν₂, ν₃, ν₄ и горизонтальные β₁, β₂ углы. Решая лежащий в горизонтальной плоскости треугольник АВС, получим значения сторон:

,

где угол γ =180º − β₁ −β_2.

Рис.48. Схема определения высоты сооружения с использованием базиса

Решая теперь треугольники A’DE и A’DC построенные в вертикальной плоскости с точки A, получим высоту сооружения H ₁= h ₁+ h ₂. Для контроля те же действия выполним и с точки В, оценивая относи­тельную погрешность по формуле (79).