 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Крок 4. Задайте параметр навчання
|
|
Використовувати для навчання мережі % вибірки…
Всі приклади, що подаються на вхід нейромережі, поділяються на дві множини – навчальну та тестову. Задайте, скільки відсотків прикладів буде використано в навчальній вибірці. Записи, що використовуються для тестування, вибираються випадково, але пропорції зберігаються.
Швидкість навчання…
Параметр визначає амплітуду корекції ваг на кожному кроці навчання.
Момент (імпульс)…
Параметр визначає ступінь впливу i-ої корекції ваг на i+1-ту.
Розпізнано, якщо помилка за прикладом <…
Якщо результат прогнозування відрізняється від значення з навчальної множини є меншим за вказану величину, то приклад вважається розпізнаним.
Використовувати тестову множину як валідаційну…
При встановлення цього прапорця, навчання буде припинено як тільки помилка на тестовій множині почне збільшуватися. Видається відповідне повідомлення. Це допомагає уникнути ситуації перенавчання нейромережі.
Критерії зупинки навчання…
Необхідно визначити момент, коли навчання буде закінчено.

Рисунок 5.9 - Параметри навчання
Крок 5. Перевірте всі задані параметри

Рисунок 5.10 - Перевірка заданих параметрів
Крок 6. Запустіть навчання системи
Пуск навчання/зупинка навчання…
Запустіть процес. В таблиці над кнопкою можна спостерігати, як міняється помилка навчання.
Розподіл помилки…
У діаграмі відображається розподіл помилки. Зелені стовпці – помилка на навчальній вибірці, червоні – на тестовій вибірці. Чим правіше стовпець, тим вище значення помилки. Шкала від 0 до 1. Чим вище стовпець, тим більше прикладів із зазначеною помилкою.
Розподіл прикладів у навчальній/тестовій вибірці…
На цих графіках можна відслідковувати наскільки результати, що спрогнозовані нейронною мережею збігаються зі значеннями в навчальній (ліворуч) і тестовій (праворуч) вибірці. Кожен приклад позначено на графіку точкою. Якщо точка попадає на виділену лінію (діагональ), то нейромережа передбачила результат з досить високою точністю. Якщо точка знаходиться вище діагоналі, значить нейромережа недооцінила результат, нижче – переоцінила. Необхідно домагатися, щоб точки розташовувалися якнайближче до діагоналі.
Крок 7. Розрахуйте кінцевий результат
У наборі вхідних параметрів введіть числа і натисніть на кнопку "Розрахунок". У таблиці «розраховані параметри» висвічується результат. Якщо результати влаштовують, то натисніть на кнопку "Зберегти". Neural Network Wizard зберігає всі параметри і налаштування у файлі з розширенням nnw.

Рисунок 5.11 - Запуск системи
Крок 8. Результат розрахунку знаходиться в файлі з розширенням.NNW.
[Network]
TeachSpeed=0.1
Miu=0.5
Alpha=1
Epoch=27612
CountLayers=3
(кількість нейронів в шарах)
Layer_0=2
Layer_1=3
Layer_2=1
% (синаптичні ваги)
% W_i_j_k – ваги синапсів (i = номер шару - 2, j – номер нейрону, k – номер синапсу даного нейрона).
W_0_0_0=1.88436421955477
W_0_0_1=1.09436537111843
W_0_0_2=2.2901761847617
W_0_1_0=1.70436421955478
W_0_1_1=0.574365371118406
W_0_1_2=2.23017618476171
W_1_0_0=4.25597733015697
W_1_1_0=3.11238189250291
W_1_2_0=3.91917004197399
WT_0_0=-3.59276885024955
WT_0_1=-1.04124724491013
WT_0_2=3.82886355094158
WT_1_0=-4.77655231133209
Контрольні питання
1. Що таке нейронна мережа і які її основні властивості?
2. Яка структура нейрона?
3. Які функції активації можуть бути використані в нейронних мережах?
4. Які вимоги пред'являються до функцій активації?
5. Які функції виконує вхідний шар в багатошаровій мережі?
Лабораторна робота №6
Нейромережеве прогнозування динамічного стану об'єктів керування
Мета: вивчення методики синтезу нейронних мереж орієнтованих на прогнозування сигналів.
ÄКороткі теоретичні відомості
Розглянемо основні принципи застосування штучної нейронної мережі ADALINE в прогнозуванні значень детермінованого процесу  . Функціональна схема настроювання ШНМ наведена на рис.6.1.
. Функціональна схема настроювання ШНМ наведена на рис.6.1.

Рисунок 6.1 – Функціональна схема настроювання ШНМ
За допомогою екстраполяції нульового порядку неперервний сигнал приводиться до дискретної бази  . Дискретний сигнал виходу об'єкту керування поступає на лінію затримки так, що на її виході формуються 2 сигнали: y(i-1), y(i-2). Настройка мережі реалізується за допомогою М-функції adapt, яка змінює параметри мережі на кожному кроці з метою мінімізації похибки e[i]= y[i] – a[i]. Якщо ця похибка нульова, то вихід мережі а[i] дорівнює y(i), тобто мережа виконує прогноз належним чином.
. Дискретний сигнал виходу об'єкту керування поступає на лінію затримки так, що на її виході формуються 2 сигнали: y(i-1), y(i-2). Настройка мережі реалізується за допомогою М-функції adapt, яка змінює параметри мережі на кожному кроці з метою мінімізації похибки e[i]= y[i] – a[i]. Якщо ця похибка нульова, то вихід мережі а[i] дорівнює y(i), тобто мережа виконує прогноз належним чином.
Нижче приведений сценарій, який призначений для вирішення завдання прогнозу сигналу на один крок вперед. Вхідний детермінований процес отриманий в результаті проходження ступінчастого сигналу через коливальну ланку.
Оскільки для формування входу застосована динамічна ланка другого порядку, то в мережі ADALINE буде використана ЛЗ з двома блоками.
З метою отримання архіву даних про об'єкт розробимо відповідно до функціональної схеми рис.6.1 структуру моделі рис.6.2.

Рисунок 6.2 – Модель для дослідження системи нейропрогнозу
Блок Zero-Order Hold бібліотеки Discrete додатку Simulink дозволяє провести дискретизацію вхідного неперервного сигналу. З метою передачі даних до основної області Command Window пакету Matlab в моделі використані блоки To Workspace (в вікні властивостей якого задають ім'я змінної) та блок Scope з наступними змінами властивостей рис.6.3.
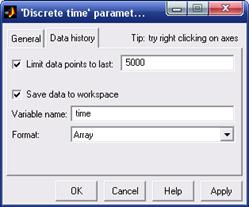
Рисунок 6.3 – Властивості блоку Scope
Запишемо наступний сценарій для вирішення задачі прогнозу сигналу.
% Вибірка з масиву часової функції блоку Scope першого стовпця (дискр. час)
time = time(:,1);
% Формування навчальної множини
p = y_i(1:length(y_i)-1)'; % вхід ШНМ з першого елементу масиву y_i
t = y_i(2:length(y_i))'; % цільовий вихід ШНМ з другого елементу масиву y_i
time = time(1:length(y_i)-1); % вибірка дискретного часу
% Формування нейронної мережі
net = newlin([-1 1],1[1 2]);
% в склад статичної НМ не включають лінії затримки та зворотні зв'язки.
% попередньою командою створюють одношарову НМ з двохелементним
% вектором входу та лінійною функцією активації. З цією метою застосована
% команда newlin яка потребує завдання мінімальне та максимальне значення
% для кожного елементу входу [-1 1] та кількість шарів (в даному випадку 1)
P = num2cell(p);
T = num2cell(t);
% папередні команди перегруповують масиви
% Настройка нейронної мережі
pi = {0 0}; % вивід синаптичних ваг на нульові рівні
net.adaptParam.passes = 5; % завдання кількості циклів навчання
% на даному етапі є можливість завдання швидкості настроювання ваг входу
% net.inputWeights{1,1}.learnParam.lr = 0.2;
% та зсуву net.biases{1,1}.learnParam.lr = 0;
[net,Y,E,Pf,Af] = adapt(net,P,T,pi); % команда виклику процедури настроювання
Y1 = cat(1,Y{:}); % конкатинація (поєднання) елементів Y{:} в вектор-стовбець
% Побудова графіків
figure(1), plot(time,Y1,'b:',time,p,'r-'), grid on
xlabel|('час, с|із|'), ylabel|('Процеси')
title|('Навчання|вчення| нейронної мережі|сіті|')
% Моделювання нейронної мережі
x = sim(net,P);
x1 = cat(1,x{:});
figure(2), plot(time,x1,'b:+', time,p,'r-o'),grid on
legend('вихід', 'вхід')
gensim(net) % виклик Simulink структури НМ
В результаті проведення даного сценарію можуть бути отримані наступні результати рис.6.4.


Рисунок 6.4 – Часові діаграми навчання та роботи НМ
Структурна-схема розробленої мережі наведена на рис.6.5.

Рисунок 6.5 - Структурна-схема розробленої НМ
На наступному кроці копіюється структура НМ в базову модель рис.6.6.

Рисунок 6.6 – Імітаційна модель для перевірки роботи розробленої ШНМ
Результати роботи НМ на інтервалі 30с наведено на рис.6.7.

Рисунок 6.6 – Візуалізація результатів для порівняння роботи ШНМ (1) з виходом об'єкту (2)
За допомогою команд net.IW{1} та net.b{1} є можливість отримати значення синаптичних ваг та відповідних зсувів:
>> net.IW{1}
ans =
0.4034 0.3384
>> net.b{1}
ans =
0.2567
Зміна вищевказаних параметрів проводиться у наступному форматі:
>> net.IW{1}=[значення];
>> net.b{1} = [значення];
У фігурних дужках вказують номера шарів НМ. Так при наявності зв'язку другого шару (три нейрона) з першим (один нейрон) формат запису буде наступним:
>> net.LW{2,1}=[значення1; значення2; значення3];
для третього, вихідного шару з одним нейроном:
>> net.LW{3,2}=[значення1 значення2 значення3];
Варіанти завдань
Необхідно:
1) Отримати завдання згідно варіанту табл. 5.1.
Таблиця 6.1 – Варіанти завдань
| # варіанту | Об'єкт | Час дискретизації | Час навчання/умова |

| 0,1 | 10с/ 
| |

| 0.2 | 10с/ 
| |

| 0,1 | 9с/ 
| |

| 0,05 | 10с/ 
| |

| 0,1 | 9с/ 
| |
| 0,1 | 10с/ 
| |

| 0,1 | 8с/ 
|
Продовження табл.6.1
| # варіанту | Об'єкт | Час дискретизації | Умови прогнозу |

| 0,01 | 10с/ 
| |
| 0,01 | 9с/ 
| |

| 0,05 | 7с/ 
| |

| 0,1 | 8с/ 
|
2) Провести параметричний та структурний синтез нейромережевої моделі об'єкту.
3) Перевірити ефективність роботи НМ на структурних моделях.
4) Розрахувати середньоквадратичну похибку роботи НМ.
5) Надати графічну ілюстрацію розробленої мережі з відповідними параметрами синаптичних зв'язків та зсувів.
6) Оформити детальний звіт.
Контрольні питання
1. Чи можна навчити нейронну мережу без прихованого шару?
2. У чому полягає навчання нейронних мереж?
3. Чому один з алгоритмів навчання отримав назву «Алгоритм зворотного розповсюдження»?
4. Чим відрізняється навчання з вчителем від навчання без вчителя?
5. Чому вхідні і вихідні сигнали нейронної мережі повинні бути нормовані, тобто приведені до діапазону [0,1]?
Індивідуальне домашнє завдання №3
Графоаналітичне рішення задач електротехніки
з нелінійними елементами

Використовуючи чисельні методи наближення функцій і рішення нелінійних рівнянь розв'язати задачі розділу: "Нелінійні ланцюги постійного і змінного струму".


Лабораторна робота № 5
Чисельні методи розрахунку визначених інтегралів.
Мета: засвоєння теоретичного матеріалу та придбання навичок коректного використання програмних пакетів для вирішення інженерних задач.
Для заданої функції обчислити визначений інтеграл по складених формулах трапецій і Сімпсона. Оцінити погрішність кожного результату.
Варіант Підінтегральна функція нижня межа верхня межа
1 (1.5*Х2+)/(Х5+1).00 1.20
2 (Х-Х3)/(Х4+2) 2.00 4.40
3 (2.2*Х+1.7)/(3.1*Х3+9.3*Х2) 1.00 2.20
4 (Х2-4.1)/(Х4+1).00 1.20
5 (3.5*Х2+Х)/(Х5+2).00 1.20
6 (1-3.7*Х)/(Х3+Х) 2.00 4.40
7 (Х3+4.5)/(Х5+5.4) 1.00 2.80
8 (2.4-Х2)/(Х3+8.1*Х) 1.00 3.40
9 (5.2*Х+4.8)/(4.5*Х3+4.1) 1.00 2.20
10 (Х2-3.7)/(Х5+1).00 1.80
11 (3.3*Х-2.8)/(4.5*Х3+7.4) 2.00 3.20
12 (Х-1.8)/(Х4+5.1).00 1.20
13 (4.2*Х2-8.1)/(Х5+3.8) 1.00 2.80
14 (1.6*Х-3.8)/(1.2*Х5+1.7) 2.00 3.20
15 (Х2-4.9)/(Х4+1.8) 1.00 2.20
16 (Х2+1.5*Х)/(Х3+7.1) 1.00 3.40
17 (1.8*Х-3.9)/(Х5+2.1).00 1.80
18 (Х2+1.8)/(Х5+7.9) 2.00 4.40
19 (3.8*Х-7.5)/(2.5*Х5+2).00 1.20
20 (1.8*Х3-1)/(Х3+7.1) 1.00 2.20
21 (3.1*Х+2.1)/(Х5+2) 2.00 3.20
22 (Х2-6.1)/(Х4+2.4) 1.00 3.40
23 (1.8-Х)/(Х3+4.8) 2.00 4.40
24 (Х2+1.9)/(Х4+3.1).00 1.20
25 (Х+3.8)/(Х5+7.1) 1.00 2.20
26 (3*Х2-1.2)/(Х5+1) 2.00 3.20
27 (Х-1.8)/(Х3+0.6).00 1.20
28 (Х2+1.6)/(Х-1.2) 1.00 2.20
29 (Х3-4.5)/(Х+1) 2.00 3.20
30 (Х4+2.7)/(Х2-0.9).00 1.80
31 (1.5*Х2)/(Х5+1).00 1.20
32 (Х-Х3)/(Х4+2) 2.00 4.40
33 (2.2*Х+1.7)/(3.1*Х3+9.3*Х2) 1.00 2.20
34 (Х2-4.1)/(Х4+1).00 1.20
35 (3.5*Х2+Х)/(Х5+2).00 1.20
36 (1-3.7*X)/(X3+X) 2.00 4.40
37 (X3+4.5)/(X5+5.4) 1.00 2.80
38 (2.4-X2)/(X3+8.1*X) 1.00 3.40
39 (5.2*X+4.8)/(4.5*X3+4.1) 1.00 2.20
40 (X2-3.7)/(X5+1).00 1.80
41 (3.3*X-2.8)/(4.5*X3+7.4) 2.00 3.20
42 (X-1.8)/(X4+5.1).00 1.20
43 (4.2*X2-8.1)/(X5+3.8) 1.00 2.80
44 (1.6*X-3.8)/(1.2*X5+1.7) 2.00 3.20
45 (X2-4.9)/(X4+1.8) 1.00 2.20
46 (X2+1.5*X)/(X3+7.1) 1.00 3.40
47 (1.8*X-3.9)/(X5+2.1).00 1.80
48 (X2+1.8)/(X5+7.9) 2.00 4.40
49 (3.8*X-7.5)/(2.5*X5+2).00 1.20
50 (1.8*X3-1)/(X3+7.1) 1.00 2.20
51 (3.1*X+2.1)/(X5+2) 2.00 3.20
52 (X2-6.1)/(X4+2.4) 1.00 3.40
53 (1.8-X)/(X3+4.8) 2.00 4.40
54 (X2+1.9)/(X4+3.1).00 1.20
55 (X+3.8)/(X5+7.1) 1.00 2.20
56 (3*X2-1.2)/(X5+1) 2.00 3.20
57 (X-1.8)/(X3+0.6).00 1.20
58 (X2+1.6)/(X-1.2) 1.00 2.20
59 (X3-4.5)/(X+1) 2.00 3.20
60 (X4+2.7)/(X2-0.9).00 1.80
61 (1.5*X2+)/(X5+1).00 1.20
62 (X-X3)/(X4+2) 2.00 4.40
63 (2.2*X+1.7)/(3.1*X3+9.3*X*X) 1.00 2.20
64 (X2-4.1)/(X4+1).00 1.20
65 (3.5*X2+X)/(X5+2).00 1.20
66 (1-3.7*X)/(X3+X) 2.00 4.40
67 (X3+4.5)/(X5+5.4) 1.00 2.80
68 (2.4-X2)/(X3+8.1*X) 1.00 3.40
69 (5.2*X+4.8)/(4.5*X3+4.1) 1.00 2.20
70 (X2-3.7)/(X5+1).00 1.80
71 (3.3*X-2.8)/(4.5*X3+7.4) 2.00 3.20
72 (X-1.8)/(X4+5.1).00 1.20
73 (4.2*X2-8.1)/(X5+3.8) 1.00 2.80
74 (1.6*X-3.8)/(1.2*X5+1.7) 2.00 3.20
75 (X2-4.9)/(X4+1.8) 1.00 2.20
76 (X2+1.5*X)/(X3+7.1) 1.00 3.40
77 (1.8*X-3.9)/(X5+2.1).00 1.80
78 (X2+1.8)/(X5+7.9) 2.00 4.40
79 (3.8*X-7.5)/(2.5*X5+2).00 1.20
80 (1.8*X3-1)/(X3+7.1) 1.00 2.20
81 (3.1*X+2.1)/(X5+2) 2.00 3.20
Лабораторна робота № 6
Чисельні методи рішення диференційних рівнянь
Мета: засвоєння теоретичного матеріалу та придбання навичок коректного використання програмних пакетів для вирішення інженерних задач.
Розв'язати диференціальне рівняння Y'=F(X)
Варіант  нтервал інтегрування початкова умова погрішність
нтервал інтегрування початкова умова погрішність
1 1+.2*Y*SIN(X)-Y2.00.50.00.01
2 COS(X+Y)+2.5*(X-Y).00.60.00.02
3 (1-Y*Y)*COS(X)+2.6*Y.00 1.00.00.05
4 COS(1.5*X+Y)+X-Y.00.50.00.01
5 1-SIN(X-Y)+1.5*(X-Y).00.60.00.02
6.6*SIN(X)-1.2*Y*Y.00 1.00.00.05
7 COS(2*X+Y)+1.5*(X-Y).00.60.00.02
8 1+.8*Y*SIN(X)-2*Y*Y.00 1.00.00.05
9 COS(X+3*Y)+X-Y.00.50.00.01
10.5*X*Y.00 1.00 1.00.00
11 X2-Y2.00 1.00.00.01
12 1-X*Y2 .00 1.00.00.01
13 SQRT(X)-.7*Y*Y 2.00 3.00 1.00.05
14 -SQRT(X*Y)+1.5 2.00 3.00 2.00.02
15.5*X-X*X*Y 3.00 4.00 1.00.05
16 SQRT(X3)+4 4.00 5.00.00.05
17 SQRT(3*X*Y)+Y2 1.00 2.00.00.05
18 X2-X*Y.00 1.00.00.01
19 SQRT(X4+4)+7.00 1.00.00.05
20 X+.8*Y2.00 1.00 1.00.01
21 SQRT(X*Y2+.7*X).00 1.00.00.02
22 1+X-Y2.00 1.00 1.00.02
23 X2-Y2 1.00 2.00.00.01
24 -X*Y-.1*Y2.00 2.00 1.00.05
25 X3-Y2.00 3.00 1.00.05
26 EXP(X)-Y2 1.00 2.00.00.05
27 X*LOG(Y)-Y*LOG(X) 2.00 2.50 1.00.05
28 2*Y-X+COS(X).00 1.00.00.05
29 2*X+COS(Y) 3.00 4.00.00.03
30 COS(X)*SIN(Y)+X*Y.00 1.00 1.50.05
31 1+.2*Y*SIN(X)-Y2.00.50.00.01
32 COS(X+Y)+2.5*(X-Y).00.60.00.02
33 (1-Y*Y)*COS(X)+2.6*Y.00 1.00.00.05
34 COS(1.5*X+Y)+X-Y.00.50.00.01
35 1-SIN(X-Y)+1.5*(X-Y).00.60.00.02
36.6*SIN(X)-1.2*Y*Y.00 1.00.00.05
37 COS(2*X+Y)+1.5*(X-Y).00.60.00.02
38 1+.8*Y*SIN(X)-2*Y*Y.00 1.00.00.05
39 COS(X+3*Y)+X-Y.00.50.00.01
40.5*X*Y.00 1.00 1.00.00
41 X2-Y2.00 1.00.00.01
42 1-X*Y2.00 1.00.00.01
43 SQRT(X)-.7*Y*Y 2.00 3.00 1.00.05
44 -SQRT(X*Y)+1.5 2.00 3.00 2.00.02
45.5*X-X*X*Y 3.00 4.00 1.00.05
46 SQRT(X3)+4 4.00 5.00.00.05
47 SQRT(3*X*Y)+Y2 1.00 2.00.00.05
48 X2-X*Y.00 1.00.00.01
49 SQRT(X4+4)+7.00 1.00.00.05
50 X+.8*Y2.00 1.00 1.00.01
51 SQRT(X*Y2+.7*X).00 1.00.00.02
52 1+X-Y2.00 1.00 1.00.02
53 X2-Y2 1.00 2.00.00.01
54 -X*Y-.1*Y2.00 2.00 1.00.05
55 X3-Y2.00 3.00 1.00.05
56 EXP(X)-Y2 1.00 2.00.00.05
57 X*ALOG(Y)-Y*ALOG(X) 2.00 2.50 1.00.05
58 2*Y-X+COS(X).00 1.00.00.05
59 2*X+COS(Y) 3.00 4.00.00.03
60 COS(X)*SIN(Y)+X*Y.00 1.00 1.50.05
61 1+.2*Y*SIN(X)-Y2.00.50.00.01
62 COS(X+Y)+2.5*(X-Y).00.60.00.02
63 (1-Y*Y)*COS(X)+2.6*Y.00 1.00.00.05
64 COS(1.5*X+Y)+X-Y.00.50.00.01
65 1-SIN(X-Y)+1.5*(X-Y).00.60.00.02
66.6*SIN(X)-1.2*Y*Y.00 1.00.00.05
67 COS(2*X+Y)+1.5*(X-Y).00.60.00.02
68 1+.8*Y*SIN(X)-2*Y*Y.00 1.00.00.05
69 COS(X+3*Y)+X-Y.00.50.00.01
70.5*X*Y.00 1.00 1.00.00
71 X2-Y2.00 1.00.00.01
72 1-X*Y2.00 1.00.00.01
73 SQRT(X)-.7*Y*Y 2.00 3.00 1.00.05
74 -SQRT(X*Y)+1.5 2.00 3.00 2.00.02
75.5*X-X*X*Y 3.00 4.00 1.00.05
76 SQRT(X3)+4 4.00 5.00.00.05
77 SQRT(3*X*Y)+Y2 1.00 2.00.00.05
78 X2-X*Y.00 1.00.00.01
79 SQRT(X4+4)+7.00 1.00.00.05
80 X+.8*Y2.00 1.00 1.00.01
81 SQRT(X*Y2+.7*X).00 1.00.00.02
82 1+X-Y2.00 1.00 1.00.02
83 X2-Y2 1.00 2.00.00.01
Лабораторна робота № 7
Чисельні методи рішення рівняння Лапласа
Мета: вивчити запропонований чисельний метод рішення рівняння Лапласа, та навчитись коректно використовувати програмні пакети для вирішення поставлених задач.
Задано квадрат 4*4 з початком координат у лівому нижньому куті і сторонами рівнобіжними координатним осям. На квадрат нанесена сітка розподілів із кроком по осях H=K=1. Вузли сітки, що лежать на сторонах (але не у вершинах), позначені в порядку обходу їх "проти годинникової стрілки", починаючи з нижньої сторони, A,B,C,D,...,J,K,L.
Необхідно скласти різницеву систему рівнянь для рішення рівняння Лапласа у внутрішніх вузлах сітки, за умови, що значення функції в граничних вузлах A,B,C,...,J,K,L задані. Різницеву систему вирішити методом Зейделя з абсолютною погрішністю не більш 0.001
Варіант Межові умови
A B C D E F G H I J K L
1 2 5 10 17 15 11 -2 -7 -10 -5 -1 1
2 2 5 10 18 17 14 2 -3 -6 -2 1 2
3 2 5 10 19 19 17 6 1 -2 1 3 3
4 2 5 10 20 21 20 10 5 2 4 5 4
5 2 5 10 21 23 23 14 9 6 7 7 5
6 2 5 10 22 25 26 18 13 10 10 9 6
7 2 5 10 23 27 29 22 17 14 13 11 7
8 2 5 10 24 29 32 26 21 18 16 13 8
9 2 5 10 25 31 35 30 25 22 19 15 9
10 3 7 13 20 17 12 -3 -9 -13 -8 -3 0
11 3 7 13 21 19 15 1 -5 -9 -5 -1 1
12 3 7 13 22 21 18 5 -1 -5 -2 1 2
13 3 7 13 23 23 21 9 3 -1 1 3 3
14 3 7 13 24 25 24 13 7 3 4 5 4
15 3 7 13 25 27 27 17 11 7 7 7 5
16 3 7 13 26 29 30 21 15 11 10 9 6
17 3 7 13 27 31 33 25 19 15 13 11 7
18 3 7 13 28 33 36 29 23 19 16 13 8
19 3 7 13 29 35 39 33 27 23 19 15 9
20 4 9 16 24 21 16 0 -7 -12 -8 -3 0
21 4 9 16 25 23 19 4 -3 -8 -5 -1 1
22 4 9 16 26 25 22 8 1 -4 -2 1 2
23 4 9 16 27 27 25 12 5 0 1 3 3
24 4 9 16 28 29 28 16 9 4 4 5 4
25 4 9 16 29 31 31 20 13 8 7 7 5
26 2 5 10 17 15 11 -2 -7 -10 -5 -1 1
27 2 5 10 18 17 14 2 -3 -6 -2 1 2
28 2 5 10 19 19 17 6 1 -2 1 3 3
29 2 5 10 20 21 20 10 5 2 4 5 4
30 2 5 10 21 23 23 14 9 6 7 7 5
31 2 5 10 22 25 26 18 13 10 10 9 6
32 2 5 10 23 27 29 22 17 14 13 11 7
33 2 5 10 24 29 32 26 21 18 16 13 8
34 2 5 10 25 31 35 30 25 22 19 15 9
35 3 7 13 20 17 12 -3 -9 -13 -8 -3 0
36 3 7 13 21 19 15 1 -5 -9 -5 -1 1
37 3 7 13 22 21 18 5 -1 -5 -2 1 2
38 3 7 13 23 23 21 9 3 -1 1 3 3
39 3 7 13 24 25 24 13 7 3 4 5 4
40 3 7 13 25 27 27 17 11 7 7 7 5
41 3 7 13 26 29 30 21 15 11 10 9 6
42 3 7 13 27 31 33 25 19 15 13 11 7
43 3 7 13 28 33 36 29 23 19 16 13 8
44 3 7 13 29 35 39 33 27 23 19 15 9
45 4 9 16 24 21 16 0 -7 -12 -8 -3 0
46 4 9 16 25 23 19 4 -3 -8 -5 -1 1
47 4 9 16 26 25 22 8 1 -4 -2 1 2
48 4 9 16 27 27 25 12 5 0 1 3 3
49 4 9 16 28 29 28 16 9 4 4 5 4
50 4 9 16 29 31 31 20 13 8 7 7 5
51 2 5 10 17 15 11 -2 -7 -10 -5 -1 1
52 2 5 10 18 17 14 2 -3 -6 -2 1 2
53 2 5 10 19 19 17 6 1 -2 1 3 3
54 2 5 10 20 21 20 10 5 2 4 5 4
55 2 5 10 21 23 23 14 9 6 7 7 5
56 2 5 10 22 25 26 18 13 10 10 9 6
57 2 5 10 23 27 29 22 17 14 13 11 7
58 2 5 10 24 29 32 26 21 18 16 13 8
59 2 5 10 25 31 35 30 25 22 19 15 9
60 3 7 13 20 17 12 -3 -9 -13 -8 -3 0
61 3 7 13 21 19 15 1 -5 -9 -5 -1 1
62 3 7 13 22 21 18 5 -1 -5 -2 1 2
63 3 7 13 23 23 21 9 3 -1 1 3 3
64 3 7 13 24 25 24 13 7 3 4 5 4
65 3 7 13 25 27 27 17 11 7 7 7 5
66 3 7 13 26 29 30 21 15 11 10 9 6
67 3 7 13 27 31 33 25 19 15 13 11 7
68 3 7 13 28 33 36 29 23 19 16 13 8
69 3 7 13 29 35 39 33 27 23 19 15 9
70 4 9 16 24 21 16 0 -7 -12 -8 -3 0
71 4 9 16 25 23 19 4 -3 -8 -5 -1 1
72 4 9 16 26 25 22 8 1 -4 -2 1 2
Лабораторна робота № 8
Застосування чисельних методів наближення функцій
і рішення нелінійних рівнянь при розрахунках задач з курсу "Електроніка".
Мета: ознайомлення з класом електротехнічних задач, котрі підлягають вирішенню за допомогою чисельних методів.
& Теоретичні відомості
Розрахунок імпульсного підсилювача для забезпечення режиму підсилення і завдання відповідної точки спокою на постійному струму.
 Алгоритм розрахунку імпульсного підсилювача.
Алгоритм розрахунку імпульсного підсилювача.
Дано: Ек(В), Rк(кОм). Статичний коефіцієнт передачі струму (bDC), коефіцієнт підсилення КU. Координати робочої точки Iк(мА), Uкэ(В) визначаються згідно статичних вхідних і вихідних характеристиках транзистора.
Рішення:
1)  2) Сумарна напруга емітера:
2) Сумарна напруга емітера:
так як  , то
, то 
3)  , 4)
, 4)  5) при КU<11,
5) при КU<11, 
6)  ; 7) для стабільної роботи схеми необхідне дотримання умови:
; 7) для стабільної роботи схеми необхідне дотримання умови: 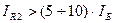 .
.
8)  , де
, де 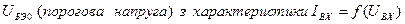
9)  , 10)
, 10)  .
.
Опис роботи:
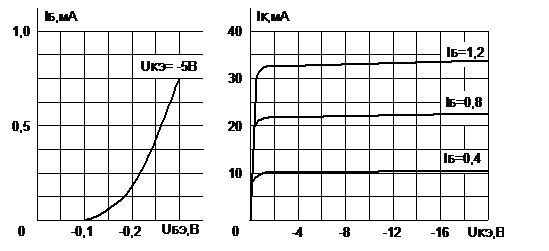 |
1. На статичних характеристиках транзистора МП40 побудувати пряму навантаження по постійному струму. Вибрати робочу точку для забезпечення А класу підсилення.
2. З використанням чисельних методів наближення функцій і рішення нелінійних рівнянь визначити координати робочої точки.
3. Розрахувати параметри імпульсного підсилювача bDC, КU, URk, UЭ, Rэ, R1, R2.
| Варіант 4 6Параметр | ||||||||||
| Eк, В | ||||||||||
| Rк, Ом |
| Варіант 4 6Параметр | ||||||||||
| Eк, В | ||||||||||
| Rк, Ом |
| Варіант 4 6Параметр | ||||||||||
| Eк, В | ||||||||||
| Rк, Ом |
| Варіант 4 6Параметр | ||||||||||
| Eк, В | ||||||||||
| Rк, Ом |
| Варіант 4 6Параметр | ||||||||||
| Eк, В | ||||||||||
| Rк, Ом |
| Варіант 4 6Параметр | ||||||||||
| Eк, В | ||||||||||
| Rк, Ом |
| Варіант 4 6Параметр | ||||||||||
| Eк, В | ||||||||||
| Rк, Ом |
4. В електронному варіанті звіту передбачити можливість програмного розрахунку варіантів з іншими вхідними даними.
Індивідуальне домашнє завдання № 4
Матрична форма запису системи диференційних рівнянь систем автоматизованого електропривода. Метод простору станів (ABCD-форма)
Скласти у векторно-матричній формі рівняння методу простору станів об'єкта з передатною функцією заданою згідно варіанту
Табл. 1. - Передатні функції
| Варіант | Передатна функція 
| |
| 1, 11 | 
| 
|
| 2, 12 | 
| 
|
| 3, 13 | 
| 
|
| 4, 14 | 
| 
|
| 5, 15 | 
| 
|
| 6, 16 | 
| 
|
| 7, 17 | 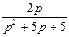
| 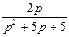
|
| 8, 18 | 
| 
|
| 9, 19 | 
| 
|
| 10, 20 | 
| 
|
Вибрати крок для чисельного рішення рівнянь і визначити початкові значення змінної стану, якщо  .
.
Розрахувати і побудувати графіки перехідного процесу, амплітудно-частотної і фазочастотної характеристики об'єкта.
Одержати дискретну передатну функцію W(z), вибравши період квантування Т. Скласти різницеве рівняння для перемінної виходу і рівняння в просторі станів. Визначити початкові значення дискретних перемінних стану.
Індивідуальне домашнє завдання № 5
Структурнй і параметричний синтез математичних моделей
двигунів постійного струму
Провести математичне моделювання двигуна постійного струму:
1) з незалежним збудженням;
2) з паралельним збудженням;
3) з послідовним збудженням.
& Короткі теоретичні відомості
Структурне моделювання електропривода.
Моделювання ДПТ з незалежним збудженням.
Індуктивність якоря:
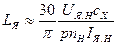
де Uя.н, Iя.н - номінальна напруга на якорі (В) і струм якоря (А), nн - номінальна швидкість обертання (об./хв), сх - емпіричний коефіцієнт (0,1 - для машин з компенсаційною обмоткою, 0,4 - для машин без компенсаційної обмотки).
Електромеханічна постійна часу:

де J - момент інерції (кгм2), Rя - опір якоря (Ом), wн - номінальна швидкість обертання (рад/с), Рн - номінальна потужність (ВТ).
Рівняння, якими описуються електромагнітні й електромеханічні процеси в двигуні приведені до безрозмірного виду і представлені в операторній формі:

де  ,
,  ,
,  ,
, 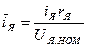 ,
,  ,
, 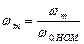 ,
, 
(відносні перемінні стану двигуна).
Параметри двигуна:  ,
,  ,
,  ,
,  .
.
Нижче наведені технічні данні двигунів постійного струму.
| Варіант | Тип | Uн, В | Рн, кВт | Iном, А | nн, об/хв | Rя, Ом | Lя, мГн | J, кг м2 | hн, % |
| ЭТ6-Р-11-6 | 1,1 | 13,8 | 0,564 | 0,037 | |||||
| ЭТ6-Р-11-6 | 2,0 | 21,4 | 0,103 | 1,8 | 0,017 | ||||
| ЭТ6-Р-11-6 | 2,1 | 23,1 | 0,235 | 7,1 | 0,083 | ||||
| ЭТ6-Р-11-6 | 2,4 | 26,1 | 0,185 | 4,2 | 0,037 | 76,5 | |||
| ЭТ6-Р-11-8 | 3,2 | 34,2 | 0,12 | 2,9 | 0,047 | ||||
| ЭТ6-Р-11-8 | 3,4 | 36,2 | 0,121 | 4,2 | 0,2 | 80,5 | |||
| ЭТ6-Р-11-11 | 3,7 | 40,3 | 0,104 | 2,4 | 0,037 | 79,5 | |||
| ЭТ6-Р-11-11 | 4,2 | 44,2 | 0,081 | 2,6 | 0,083 | 83,5 | |||
| ЭТ6-Р-11-11 | 4,5 | 47,3 | 0,084 | 3,1 | 0,2 | 82,5 | |||
| ЭТ6-Р-11-14 | 5,3 | 54,7 | 0,044 | 1,6 | 0,1 | 85,5 | |||
| ЭТ6-Р-11-19 | 5,6 | 29,2 | 0,26 | 10,2 | 0,229 | ||||
| ЭТ6-Р-11-19 | 6,0 | 30,7 | 0,145 | 4,5 | 0,083 | 86,5 | |||
| ЭТ6-Р-11-19 | 7,1 | 36,3 | 0,15 | 5,5 | 0,2 | 86,5 | |||
| ЭТ6-Р-11-19 | 40,6 | 0,125 | 5,3 | 0,3 | 87,5 | ||||
| ЭТ6-Р-11-19 | 8,1 | 41,7 | 0,044 | 1,6 | 0,1 | 86,5 | |||
| ЭТ6-Р-11-25 | 9,5 | 48,1 | 0,084 | 3,1 | 0,2 | ||||
| ЭТ6-Р-11-25 | 55,6 | 0,065 | 2,6 | 0,229 | |||||
| ЭТ6-Р-11-25 | 56,2 | 0,083 | 3,7 | 0,3 | 88,5 |
В якості постійних параметрів двигуна прийняти наступні: Тв=0,5; к'ф=1,23,
Дата публикования: 2014-11-04; Прочитано: 617 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
