 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Статистичні методи обробки експертної інформації
|
|
Статистичні методи базуються на припущенні, що відхилення оцінок експертів від істинних значень відбувається у силу випадкових причин. Експертиза 1 (Е1):  ,
,  – експерти ізольовані,
– експерти ізольовані,  – обернений зв'язок відсутній,
– обернений зв'язок відсутній,  . Тобто результуюча числова оцінка
. Тобто результуюча числова оцінка  знаходиться за формулою середньозваженого значення (математичного сподівання випадкової величини). За степінь узгодженості думок експертів служить дисперсія:
знаходиться за формулою середньозваженого значення (математичного сподівання випадкової величини). За степінь узгодженості думок експертів служить дисперсія: 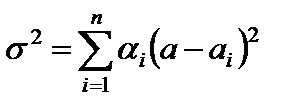 . Як модифікація (Е1) розглядається наступна експертиза 2:
. Як модифікація (Е1) розглядається наступна експертиза 2:  ,
,  =
= 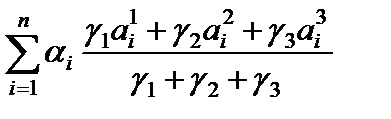 , де
, де  – "оптимістична" оцінка
– "оптимістична" оцінка  -го експерта,
-го експерта,  – "реалістична" і
– "реалістична" і  – "песимістична". Для експерта – "реаліста" (психологічний тип експерта можна визначити відповідним тестуванням) доцільно покладати
– "песимістична". Для експерта – "реаліста" (психологічний тип експерта можна визначити відповідним тестуванням) доцільно покладати  ,
,  ,
,  ; для експерта – "оптиміста"
; для експерта – "оптиміста"  ,
,  ,
,  (він "завищує" оптимістичну оцінку), для експерта – "песиміста"
(він "завищує" оптимістичну оцінку), для експерта – "песиміста"  ,
,  ,
,  (він "занижує" оптимістичну оцінку). Степінь узгодженості між оцінками визначається величиною
(він "занижує" оптимістичну оцінку). Степінь узгодженості між оцінками визначається величиною  , де
, де  ,
,  – степінь невпевненості
– степінь невпевненості  -го експерта у своїй оцінці (для експерта реаліста
-го експерта у своїй оцінці (для експерта реаліста  , для інших –
, для інших –  ). В експертизах
). В експертизах 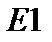 ,
,  можна визначити статистичну значимість отриманих результатів. Задаємо ймовірність похибки
можна визначити статистичну значимість отриманих результатів. Задаємо ймовірність похибки  , вважаючи, що величина
, вважаючи, що величина  розподілена за нормальним законом з центром
розподілена за нормальним законом з центром  і дисперсією
і дисперсією  . Тоді:
. Тоді:  , де
, де  , величина
, величина  має розподіл Ст'юдента з
має розподіл Ст'юдента з  -м ступенем свободи (визначаємо за таблицею розподілу Ст'юдента, за величиною р).
-м ступенем свободи (визначаємо за таблицею розподілу Ст'юдента, за величиною р).
Дата публикования: 2014-11-04; Прочитано: 718 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
