Теперь решим задачу по выборке В. 1 страница

Находим и . Размах (81 - 60+1 = 22) достаточно большой, поэтому составим вариационный ряд по интервалам значений, используя при выборке заданные начало первого интервала и длину интервала (таблица 5)

Таблица 5.

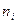
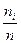
интервалы			Накопленные частости
59 − 61		0,005	0,005
61 − 63		0,010	0,015
63 − 65		0,035	0,050
65 − 67		0,080	0,130
67 − 69		0,135	0,265
69 − 71		0,200	0,465
71 − 73		0,190	0,655
73 − 75		0,190	0,845
75 − 77		0,090	0,935
77 − 79		0,045	0,980
79 − 81		0,015	0,995
81 − 83		0,005	1,000
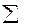
		1,000	−

При построении графиков откладываем по оси Ох значения с 59 по 83 и по оси 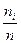− значения с 0 по 0,2 (рис. 8 и рис. 9).

Рис. 8. Полигон вариационного ряда выборки В.	Рис. 9. Гистограмма вариационного ряда выборки В.

Далее учитываем, что в качестве представителя каждого интервала взят его конец. Принимая за координаты точек концы и соединяя эти точки прямыми, построим график эмпирической функции распределения (рис.10).

Рис. 10. График эмпирической функции распределения выборки В.

Для вычисления среднего арифметического и дисперсии по формулам:

и

по таблице 5 определим с = 70 и = 2.

Суммы вычислим с помощью таблицы 6.

Таблица 6.

Интервал	Середина интервала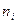
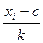
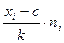
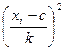
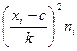
59 − 61			-5	-5
61 − 63			-4	-8
63 − 65			-3	-21
65 − 67			-2	-32
67 − 69			-1	-27
69 − 71
71 − 73
73 − 75
75 − 77
77 − 79
79 − 81
81 − 83
	−		−		−

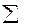
Итак, вычисляем среднее арифметическое и дисперсию:

Стандартное отклонение

Моду находим по формуле

Медиану 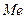находим по формуле , где

− начало медианного интервала, т.е. интервала, в котором содержится серединный элемент;

− длина медианного интервала;

− объем выборки;

− сумма частот интервалов, предшествующих медианному;

− частота медианного интервала.

Задача 2.2. Вычислить несмещенные оценки параметров генеральной совокупности , S , S по выборкам А и В, используя результаты, полученные в задаче 2.1.

Для выборки А при решении задачи 2.1. была получена несмещенная оценка значения , а также выборочная дисперсия

По формуле находим несмещенные оценки дисперсии и стандартного отклонения:

, , .

Для выборки В имеем

, ,

,

ПРИЛОЖЕНИЕ 6.

ВАРИАНТ 0

Выборка А0

2 4 2 4 3 3 3 2 0 6 1 2 3 2 2 4 3 3 5 1

0 2 4 3 2 2 3 3 1 3 3 3 1 1 2 3 1 4 3 1

7 4 3 4 2 3 2 3 3 1 4 3 1 4 5 3 4 2 4 5

3 6 4 1 3 2 4 1 3 1 0 0 4 6 4 7 4 1 3

N = 79 Начало первого интервала:0 Длина интервала:1

Выборка В0

N = 200 Начало первого интервала: 59 Длина интервала: 2.

ВАРИАНТ 1

Выборка А1

0 4 2 0 5 1 1 3 0 2 2 4 3 2 3 3 0 4 5 1

3 1 5 2 0 2 2 3 2 2 2 6 2 1 3 1 3 1 5 4

5 5 3 2 2 0 2 1 1 3 2 3 5 3 5 2 5 2 1 1

2 3 4 3 2 3 2 4 2

N = 69 Начало первого интервала:0 Длина интервала:1

Выборка В1

N = 181 Начало первого интервала:102 Длина интервала:4

ВАРИАНТ 2

Выборка А2

N = 66 Начало первого интервала: 0 Длина интервала: 1.

Выборка В2

N = 213 Начало первого интервала: 62 Длина интервала: 4.

ВАРИАНТ 3

Выборка А3

N = 82 Начало первого интервала:0 Длина интервала:1

Выборка В3

—29	— 22	—16	—20	—16	—18	—28	—20	—32	—22	—23	—26	—10	—25	—25
—29	—29	—19	—12	—26	—18	—20	—9	—24	—20	—19	—26	—23	—11	—26
—30	—23	—30	—18	—20	—13	—17	—24	—28	—26	—21	—21	—26	—24	—36
—23	—24	—25	—20	—23	—17	—11	—22	—19	—19	—25	—29	—23	—16	—25
—15	—18	—17	—19	—21	—12	—24	—30	—33	—22	—15	—18	—26	—22	—19
—25	—23	—21	—22	—22	—25	—16	—25	—19	—17	—30	—13	—25	—19	—24
—17	—24	—16	—23	—15	—22	—22	—19	—20	—19	—33	—14	—17	—21	—16
—24	—13	—20	—19	—17	—13	—27	—25	—25	—19	—22	—22	—22	—23	—9
—11	—22	—24	—18	—19	—18	—31	—16	—18	—24	—14	—23	—26	—25	—19
—23	—24	—21	—26	—25	—18	—16	—30	—16	—24	—13	—14	—18	—22	—22
—28	—18	—21	—27	—31	—23	—23	—27	—21	—21	—22	—34	—24	—20	—24
—21	—32	—16	—18	—15	—22	—15	—15	—22	—18	—	—	—	—	—

N = 175 Начало первого интервала: — 37 Длина интервала: 2

ВАРИАНТ 4

Выборка А4

N = 70 Начало первого интервала:0 Длина интервала:1

Выборка В4