Формулы алгебры логики

Любые высказывания, полученные из элементарных высказываний, с помощью конечного числа введенных логических операций, называются формулами алгебры логики.

Логические операции подчиняются определенным законам. Рассмотрим их для операций дизъюнкции и конъюнкции, учитывая свойство двойственности. Двойственность операций заключается в том, что если в формуле, содержащей только операции дизъюнкции, конъюнкции и инверсии, заменить Ù и Ú на Ú и Ù соответственно, а 0 на 1 и 1 на 0, то получаются новые равносильности.

Законы Де Моргана называют переносом через логические связки. Приведем формулы с другими операциями, которые также будем считать основными.

-снятие двойного отрицания

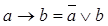- снятие импликации

Все эти формулы получаются простой проверкой по таблице истинности с учетом истинности каждой операции, правильного раскрытия скобок и выполнения операций по приоритету.

Формула называется тождественно истинной или тавтологией, если она реализует функцию «тождественная единица».

Формулы логики, принимающие всегда ложное значение, называются тождественно ложными (или противоречиями).

Например, формула - противоречие.

Для упрощения формул, содержащих скобки и различные логические операции, будем учитывать ряд правил. Так, при опускании скобок:

• самой первой выполняется конъюнкция между элементарными высказываниями и их отрицаниями;

• дизъюнкция выполняется раньше импликации и эквиваленции;

• знак отрицания над формулой дает возможность опустить скобки, в которых эта формула заключена.

С помощью основных таблиц истинности можно составлять таблицы истинности сложных формул.

Пример 1.

x1	x2

Пример 2

x1	x2

Пример 3

x1	x2

Пример 4

x1	x2

Пример 5

x1	x2

Две формулы алгебры логики называются равносильными, если они принимают одинаковые логические значения при любом наборе значений элементарных высказываний, входящих в них.

Справедливость логических равенств доказывается путем вычисления значения левой и правой частей выражения для всех возможных значений логических переменных. Если значения обеих частей выражения совпадают, то равенство считается доказанным.

Пример 6

Проверить справедливость равенства с помощью таблиц истинности

a	b

Пользуясь законами и свойствами логических функций, их можно преобразовывать

Пример 7

Пример 8

Упражнения

1. Проверьте справедливость равенства с помощью таблиц истинности

2. Постройте таблицы истинности формул

а)

б)

3. Пользуясь законами и свойствами логических функций, преобразуйте формулу