 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Тема 2.2. Сложные высказывания
|
|
Математическая логика
Тема 2.1. Высказывания
Суждения как форма мышления
Я знаю только то, что я ничего не знаю, другие не знают и этого.
Сократ
Суждением называется форма мышления, в которой что-либо утверждается или отрицается о существовании предмета, связях между предметом и его свойствами или об отношениях между предметами.
Словам естественного языка, например русского, в логике соответствуют понятия. Слова объединяются в предложения. По интонации предложения делятся на вопросительные, восклицательные и повествовательные. Но информацию несут только повествовательные предложения. Таким предложениям в логике соответствуют суждения. Они выражают наши знания о связях между понятиями. Суждение характеризуют две стороны: его форма и его истинность. Отвлечемся от формы и рассмотрим вопрос о том, истинно оно или ложно.
Под высказыванием понимается любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности. Каждое высказывание либо истинно либо ложно. Значение «истина» обозначается 1, значение «ложь» - 0.
Примеры:
Дважды два – пять
Уфа – столица Башкортостана
Рассмотрим примеры повествовательных предложений.
1. Умение грамотно использовать логические операции повышает эффективность программирования.
2. История логики насчитывает около двух с половиной тысячелетий.
3. Знание математической логики необходимо любому специалисту.
4. Математическая логика — увлекательная наука.
5. х> 5.
6. Была метель.
7. Он — программист.
Предложения 1, 2, 3 являются высказываниями, а 4 и 5 — нет. Однозначно для всех людей определить отношение к науке невозможно, так же как невозможно определить истинность неравенства х> 5, не зная значений переменной х, входящей в него. Не является высказыванием и предложение 6, так как нет достаточной информации, чтобы установить, истинно оно или ложно (где и когда?). Однако предложение х > 5 может стать высказыванием, если будут известны конкретные значения переменной х. Так, если задать множество значений х: х Î {О, 2, 5, 7, 12}, то высказывания 0>5, 2>5, 5>5 будут ложными, а 7>5, 12 > 5 — истинными. Истинными будут высказывания 1 и 2, ложным — третье, так как есть множество профессий, для которых знания математической логики не обязательны. Предложение «Он — программист» станет высказыванием при подстановке вместо местоимения «он» имени отдельного человека. Используя кванторные слова «всякий», «некоторый», «есть» и др., тоже можно получить высказывания. Например, «Всякий человек есть программист» — ложное высказывание. Заметим, что предложения вида 5 и 7 подробно изучает логика предикатов, с которой мы познакомимся позже.
Формализацией высказываний называют операцию замены высказывания естественного языка формулой математического языка, включающего высказывательные переменные и символы тех логических операций, которые соответствуют структуре самого высказывания.
Булевы функции
Мы употребляем знаки не только для того, чтобы передавать наши мысли другим людям, но и для того, чтобы облегчить сам процесс нашего мышления.
Г. В. Лейбниц
 Джордж Буль George Boole
(02.11.1815 – 08.12.1864) Джордж Буль George Boole
(02.11.1815 – 08.12.1864)
| Джордж Буль родился в Линкольне (Англия) в семье мелкого торговца. Материальное положение его родителей было тяжелым, поэтому Джордж смог окончить только начальную школу для детей бедняков; в других учебных заведениях он не учился. Этим отчасти и объясняется, что, не связанный традицией, он пошел в науке собственным путем. Буль самостоятельно изучил латынь, древнегреческий, немецкий и французский языки, изучил философские трактаты. С ранних лет Буль искал работу, оставляющую возможности для самообразования. После многих неудачных попыток Булю удалось открыть маленькую начальную школу, в которой он преподавал сам. Школьные учебники по математике привели его в ужас своей нестрогостью и нелогичностью, Буль вынужден был обратиться к сочинениям классиков науки и самостоятельно проштудировать обширные труды Лапласа и Лагранжа. |
В связи с этим занятием у него появились первые самостоятельные идеи. Результаты своих исследований Буль сообщил в письмах профессорам математики (Д.Грегори и А.де Моргану) знаменитого Кембриджского университета и вскоре получил известность как оригинально мыслящий математик. В 1849 году в г.Корк (Ирландия) открылось новое высшее учебное заведение – Куинз колледж, по рекомендации коллег-математиков Буль получил здесь профессуру, которую сохранил до своей смерти в 1864 году.
Только здесь он получил возможность не только обеспечить родителей, но и спокойно, без мыслей о хлебе насущном, заниматься наукой. Здесь же он женился на дочери профессора греческого языка Мери Эверест, которая помогала Булю в работе и оставила после его смерти интересные воспоминания о своем муже; она стала матерью четырех дочерей Буля, одна из которых, Этель Лилиан Буль, в замужестве Войнич, - автор популярного романа "Овод".
Джордж Буль по праву считается отцом математической логики. Его именем назван раздел математической логики - булева алгебра. В 1848 году Джордж Буль опубликовал статью по началам математической логики - "Математический анализ логики, или Опыт исчисления дедуктивных умозаключений", а в 1854 году появился главный его труд "Исследование законов мышления, на которых основаны математические теории логики и вероятностей". В этих работах отразилось убеждение Буля о возможности изучения свойств математических операций, осуществляемых не обязательно над числами. Ученый говорил о символическом методе, который он применял как к изучению дифференцирования и интегрирования, так и к логическому выводу и к теоретико-вероятностным рассуждениям. Именно он построил один из разделов формальной логики в виде некоторой "алгебры", аналогичной алгебре чисел, но не сводящейся к ней.
Буль изобрел своеобразную алгебру - систему обозначений и правил, применимую ко всевозможным объектам, от чисел до предложений. Пользуясь этой системой, он мог закодировать высказывания (утверждения, истинность или ложность которых требовалось доказать) с помощью символов своего языка, а затем манипулировать ими, подобно тому как в математике манипулируют числами. Основными операциями булевой алгебры являются конъюнкция (И), дизъюнкция (ИЛИ), отрицание (НЕ). Через некоторое время стало понятно, что система Буля хорошо подходит для описания электрических переключателей схем. Ток в цепи может либо протекать, либо отсутствовать, подобно тому как утверждение может быть либо истинным, либо ложным. А еще несколько десятилетий спустя, уже в ХХ столетии, ученые объединили созданный Джорджем Булем математический аппарат с двоичной системой счисления, заложив тем самым основы для разработки цифрового электронного компьютера.
Алгебра логики, выстроенная в XIX в., долго существовала как абстрактная, хотя и очень красивая наука. Но в середине XX в. оказалось, что она имеет конкретное и очень важное применение в современной жизни. Булева алгебра в настоящее время служит основой для описания логики работы аппаратных и программных средств ЭВМ. Дело в том, что алгебра логики использует логические переменные, которые принимают лишь два значения 0 и 1. Аналогично ЭВМ, используя лишь сигналы 0 и 1, воспринимает их как двоичные числа или логические переменные.
Алгебра логики (булева алгебра)– это раздел математической логики, значения всех элементов которой определены в двухэлементном множестве. Алгебра логики оперирует логическими высказываниями.
Булевы переменные (логические переменные) – это переменные, имеющие только два значения false (ложь) и true (истина).
Булевой (логической) функцией называется такая функция, аргументами которой являются булевы переменные, и сама функция принимает значение из множества ноль и единица.Простейшими операциями алгебры логики являются операции логического сложения (дизъюнкция, операция ИЛИ), логического умножения (конъюнкция, операция И). Для обозначения логического сложения используются символы «+», « », для логического умножения – «∙», «
», для логического умножения – «∙», « ». В алгебре логики используется еще одна операция- операция отрицания (инверсия, операция НЕ). Обозначается
». В алгебре логики используется еще одна операция- операция отрицания (инверсия, операция НЕ). Обозначается 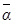 ,
, 
Примеры.
Пусть a и b – некоторые высказывания, тогда логические операции над высказываниями записываются следующим образом:
a+b или a  b
b
a∙b или a  b
b
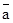 или
или 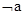
Пусть переменная x логическая переменная, т. е. может принимать одно из 2-х возможных значений: «истина» (1), «ложь» (0). Тогда функция от переменной x называется логической функцией.
Пример.
F(x1, x2)=x1 

f(x)= 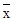
Элементарные логические функции задаются табличным способом, то есть для каждой логической функции строится так называемая таблица истинности.
1) Инверсия. Инверсией (логическим “ не ”) высказывания Р называется высказывание, которое истинно только тогда, когда высказывание Р ложно. Обозначается 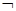 Р или
Р или  .
.
Соответствие между высказываниями определяется таблицами истинности. В нашем случае эта таблица имеет вид:
| P | 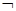 Р Р
|
2) Конъюнкция. Конъюнкцией (логическим “ и ”) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания. Обозначается P&Q или 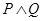 .
.
| P | Q | 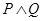
|
3) Дизъюнкция. Дизъюнкцией (логическим “ или ”) двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба высказывания ложны. Обозначается P˅Q.
| P | Q | 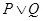
|
4) Импликация. Импликацией (логическим следованием) двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда высказывание Р истинно, а Q – ложно. Обозначается PÉQ (или Р 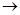 Q). Высказывание Р называется посылкой импликации, а высказывание Q – следствием.
Q). Высказывание Р называется посылкой импликации, а высказывание Q – следствием.
| P | Q | P 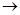 Q Q
|
5) Эквиваленция. Эквиваленцией (логической равносильностью) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинности высказываний совпадают. Обозначается Р~Q или Р«Q.
| P | Q | P«Q |
Тема 2.2. Сложные высказывания
Дата публикования: 2015-11-01; Прочитано: 1116 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
