Перетин двох площин

В. В. Хорошайло, О. В. Жартовський

НАРИСНА ГЕОМЕТРІЯ

НАВЧАЛЬНІ ЗАВДАННЯ
ДО ПРАКТИЧНИХ ЗАНЯТЬ
І САМОСТІЙНОЇ РОБОТИ

(для студентів технічних спеціальностей)

Затверджено

на засіданні вченої ради

Протокол № 11 від 1.07.2014

Краматорск 2014

УДК 514.18

ББК 22.151.3

Н 40

Рецензенти:

Козлов В. І., професор, проректор з науково-методичної роботи ДІТМ;

Бившев О. П., професор, КЕГІ.

Хорошайло, В. В.

Н 40 Нарисна геометрія: навчальні завдання до практичних занять і самостійної роботи / В. В. Хорошайло, О. В. Жартовський. – Краматорськ: ДДМА, 2014. – 36 с.

ISBN 978-966-379-282-8.

Наведено практичні задачі з нарисної геометрії та питання для самопідготовки.

УДК 514.18

ББК 22.151.3

ISBN 978-966-379-282-8

© В. В. Хорошайло; О. В. Жартовський, 2014 © ДДМА

ЗМІСТ

Умовні позначення............................................................................................................
1 Проекціювання точки, прямої та площини на дві і три площини проекцій…….
2 Розташування прямої відносно площин проекцій………………………………….
3 Належність точки і прямої площині. Різне розташування площин відносно площин проекцій. Кути нахилу площини загального розташування до площин проекцій…………………………………………………………………..
4 Перетин прямої з площиною. Перетин двох площин.
5 Паралельність і перпендикулярність прямої і площини, двох площин………….
6 Метод заміни площин проекцій………………………………………………….....
7 Точка та лінія на поверхні………………………………………………………..…
8 Переріз тіл площиною. Визначення натуральної величини перерізу…………….
9 Перетин прямої з поверхнею………………………………………………………..
10 Аксонометрія
11 Комплексне креслення тіл з крізним отвором……………………………………..
12 Побудова розгорток поверхонь…………………………………………………….
13 Взаємний перетин багатогранників………………………………………………..
14 Перетин кривої та багатогранної поверхонь………………………………………
15 Перетин кривих поверхонь
16 Самостійна робота для підготовки до модульного контролю.
Література………………………………………………………………………………..

Умовні позначення

1 Точки простору позначаються великими літерами латинського алфавіту або цифрами: А, B, С, D …; 1, 2, 3, 4...

2 Лінії (прямі і криві) простору – малими літерами латинського алфавіту:
a, b, c, d...

3 Поверхні – великими літерами грецького алфавіту: Γ, Φ, Σ, Ω …

4 Кути – малими літерами грецького алфавіту: α, β, γ, φ...

5 Площини проекцій позначаються так:

П₁ – горизонтальна;

П₂ – фронтальна;

П₃ – профільна;

П₄, П₅, П₆ – додаткові площини проекцій (Π – велика грецька літера “ пі ”).

6 Проекції точок, ліній та поверхонь позначаються так само, як і їх оригінали з доданням індексу, відповідного індексу площини проекцій. Проекції точки А, лінії a, площини Σ позначаються так:

на площину П₁ – А₁, а₁, Σ ₁;

на площину П₂ – А₂, а₂, Σ ₂;

на площину П₃ – А₃, а₃, Σ ₃.

7 Деякі прямі і площини мають постійні позначення.

Лінії рівня: горизонталь – h, фронталь – f, профільна пряма – p.

Площини рівня: горизонтальна – Г, фронтальна – Ф.

8 Основні операції позначаються:

збіг – ≡; перетин (переріз) – ∩;

паралельність – ║; схрещуваність – ;

перпендикулярність – ; відображення – →;

належність – ; логічний наслідок – .

1 ПРОЕКЦІЮВАННЯ ТОЧКИ, ПРЯМОЇ ТА ПЛОЩИНИ

НА ДВІ І ТРИ ПЛОЩИНИ ПРОЕКЦІЙ

1 Розкрити суть центрального та паралельного проекціювань.

2 Що таке лінія зв’язку? Що таке проекція точки?

3 Яке креслення називається комплексним?

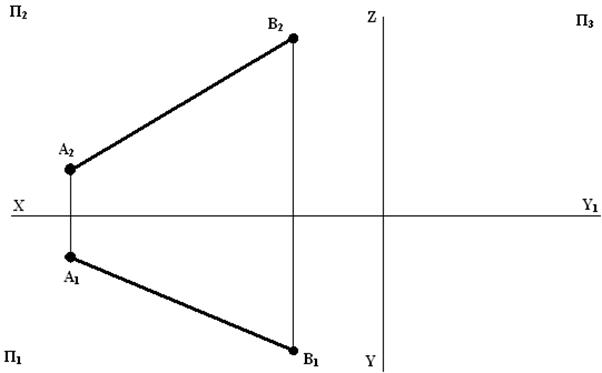
Задача1. За двома проекціями точки побудувати третю. Виміряти та записати координати точок. Побудувати наочні зображення точок.

	A	B	C	D	E	F
X
Y
Z

Задача 2. Побудувати: а) проекції точки А, якщо відстань від неї до площини П2 дорівнює 10 мм; б) проекції точки В, якщо вона знаходиться на 8 мм нижче, на 15 мм ближче до спостерігача, ніж точка А.

Задача 3. Побудувати три проекції відрізка за координатами його кінців: A (25, 20, 28), B (12, 10, 0).

2 РОЗТАШУВАННЯ ПРЯМОЇ ВІДНОСНО ПЛОЩИН ПРОЕКЦІЇ

1 Дати визначення прямих загального та особливого розташувань.

2 Сформулювати теорему про проекціювання прямого кута.

3 Сформулювати правила визначення натуральної величини відрізка загального розташування методом прямокутного трикутника та кутів нахилу цього відрізка до площин П₁ та П₂.

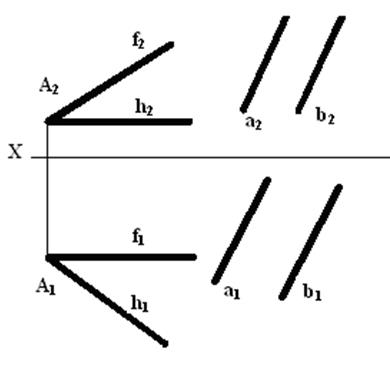
Задача 4. Для зображених відрізків рівня визначити їх розташування, натуральні величини та кути їх нахилів до площин П₁, П₂, П₃ ( – відповідно).

Відповідь:

а) АВ || П₁; н.в. АВ = 21 мм; АВ ^ П₁ = º, АВ ^ П₂ = º, АВ ^ П₃ = º;

б)

в)

а) б) в)

Завдача 5. Через точку К побудувати відрізки АВ, СD та EF(у трьох проекціях, перпендикулярні П₁, П₂ та П₃ відповідно. Вказати видимість конкуруючих точок. Записати символічно їх розташування та назву за прикладом.

Відповідь: а) АВ П₁ – горизонтально проекціювальний;

СD

EF

a) б) в)

Задача 6. Знайти натуральну величину відрізка АВ та кути його нахилу до площин П₁, П₂ та П₃. Від нижньої точки відкласти відрізок довжиною 20 мм. Навести алгоритм розв’язання задачі.

Задача 7. Через точку А побудувати прямі: а) l – паралельну а; б) m – перетинну з а; в) n– перехресну до а. Вказати, де необхідно, конкуруючі точки.

а) б) в)

Задача 8. Визначити відстань від точки К до прямої АВ. Навести алгоритм розв’язання задачі.

а) б)

Самостійна робота.

Дано: координати точок А, В та С.

Визначити:

I) довжину відрізка прямої [АВ];

2) величину кутів a і b нахилу прямої [АВ] до площин проекцій П₁ і П₂;

3) пряму l, що проходить через точку С и паралельну прямій [АВ];

4) пряму горизонтального рівня h, що проходить через точку С та перетинає [АВ ].

Завдання за варіантом виконувати на ватмані формату А3. Проекції відрізка прямій [АВ] і точки С побудувати по координатах точок відповідно до варіанта завдання, вибравши вісь X, початок координат O і масштаб так, щоб зображення зайняло більшу частину поля креслення.

Варіанти завдань:

Варіант 1 A (40, 5, 55); B (0, 50, 10); C (65, 20, 30).

Варіант 2 A (20, 10, 20); B (75, 25, 50); C (90, 85, 40).

Варіант 3 A (85,20, 80); B (25, 40, 20); C (90, 90, 60).

Варіант 4 A (85, 42, 0); B (25, 62, 20); C (0, 10, 15).

Варіант 5 A (10, 20, 25); B (55, 50, 10); C (80, 0, 20).

Варіант 6 A (65, 25, 70); B (0, 40, 40); C (90, 90, 50).

Варіант 7 A (40, 70, 5); B (0, 30, 30); C (65, 25, 25).

Варіант 8 A (42, 72, 0); B (0, 32, 33); C (75, 40, 10).

Варіант 9 A (55, 0, 30); B (0, 10, 60); C (5, 55, 45).

Варіант 10 A (45, 55, 10); B (0, 25, 35); C (60, 10, 25).

Варіант 11 A (45, 0, 60); B (80, 45, 15); C (15, 10, 35).

Варіант 12 A (0, 65, 0); B (15, 20, 50); C (0, 10, 20).

Варіант 13 A (25, 30, 50); B (65, 50, 10); C (10, 60, 40).

Варіант 14: A (88, 50, 10); B (62, 0, 60); C (20, 0, 30).

Варіант 15 A (0, 50, 10); B (25, 0, 60); C (70, 5, 30).

Варіант 16 A (105, 0, 95); B (80, 75, 30); C (0, 30, 50).

Варіант 17 A (40, 65, 20); B (0, 10, 50); C (55, 20, 40).

Варіант 18 A (70, 20, 10); B (25, 50, 30); C (0, 10, 20).

Варіант 19 A (0, 15, 40); B (60, 60, 75); C (85, 45, 60).

Варіант 20 A (35, 70, 0); B (60, 40, 20); C (20, 25, 15).

Варіант 21 A (25, 5, 70); B (65, 30, 30); C (0, 45, 40).

Варіант 22 A (25, 15, 60); B (65, 50, 15); C (0, 80, 25).

Варіант 23 A (70, 25, 5); B (15, 55, 35); C (20, 5, 20).

Варіант 24 A (15, 17, 0); B (60, 40, 20); C (0, 25, 10).

Варіант 25 A (30, 55, 5); B (75, 10, 50); C (5, 0, 20).

Варіант 26 A (0, 10, 55); B (15, 60, 10); C (70, 30, 15).

3 ПЛОЩИНА У ПРОСТОРІ. ТОЧКИ І ПРЯМІ У ПЛОЩИНІ

1 Дати визначення площини загального і особливого положення.

2 Назвати основні властивості проекціювальних площин і площин рівня.

3 Як визначити на комплексному кресленні належність точки (прямої) площині?

Завдача 9. Визначити розташування та площу прямокутника АВСD.

а) б) в)

Відповідь:

а) б) в)

Завдання 10. Визначити розташування, площу прямокутника АВСD та кути його нахилу до площин проекцій, вказати видимість точок.

а) б) в)

Відповідь:

а) б) в)

Завдання 11. Побудувати необхідні проекції точок А та В, які належать площині Σ (l ∩ m), з використанням двох ознак належності прямої площині. Кожну ознаку використати на окремому рисунку. Навести алгоритм розв’язання задачі.

а) б)

Задача 12. Додати до існуючих об’єктів геометричні об’єкти, необхідні для створення вказаних площин.

4 ПЕРЕТИН ПРЯМОЇ З ПЛОЩИНОЮ

ПЕРЕТИН ДВОХ ПЛОЩИН.

1 Як побудувати лінію перетину площини рівня з площиною загального розташування?

2 Як називаються лінії перетину загального розташування з площинами рівня?

3 Як побудувати точку перетину прямої загального розташування з проекціювальною площиною?

4 Сформулювати алгоритм побудови лінії перетину двох площин загального розташування.

Задача 13. Визначити точки перетину прямої a з фронтально проекціювальною площиною Ф та горизонтально проекціювальною площиною Σ.

Задача 14. Побудувати лінію перетину площини, заданої ΔАВС, горизонтально проекціювальною площиною Σ.

Задача 15. Побудувати лінію перетину площини, заданої ΔАВС, фронтально проекціювальною площиною Ф.

Задача 16. Побудувати лінію перетину площини Σ (l || m) фронтально проекціювальною прямою а.

Задача 17. Визначити точку перетину прямої та площини, вказати видимість прямої. Навести алгоритм розв’язання задачі.

а) б)

Задача 18. Побудувати лінію перетину двох площин та показати видимість трикутників. Навести алгоритм розв’язання задачі.

5 ПАРАЛЕЛЬНІСТЬ І ПЕРПЕНДИКУЛЯРНІСТЬ

ПРЯМОЇ І ПЛОЩИНИ, ДВОХ ПЛОЩИН

1 Як визначити, чи паралельні дана пряма і площина?

2 Сформулювати алгоритм побудови перпендикуляра до площини загального розташування.

3 Як визначити відстань від точки до прямої, від точки до площини?

4 Сформулювати алгоритм побудови площини, перпендикулярної заданій площині.

Задача 19. Побудувати через точку А пряму l., паралельну площині Σ (а || в).

Задача 20. Побудувати через точку А горизонтальну пряму, паралельну площині Σ (а || в).

Задача 21. Визначити, чи паралельна пряма а площині Σ (N; b).

Задача 22. Визначити, чи паралельна пряма аплощині Σ (А; В; С).

Задача 23.Визначити, чи паралельні наведені площини.

Задача 24. Визначити відстань від точки D до площини Σ (А;В;С). Побудувати точку, симетричну точці D відносно площини. Навести алгоритм розв’язання задачі.

Самостійна робота За заданими координатами точок A, B, С, D здійснити наступне:

1 Визначити відстань від точки D до площини (АВС).

2 Побудувати точку D^/, симетричну точці D відносно площини (АВС).

3 Знайти площу трикутника АВС.

Робота виконується на ватмані формату А3 за варіантами індивідуального завдання. Рекомендується використовувати методичні вказівки по виконанню РГР 1, загальним методом.

Координати точок: А (___,___,___);

В (___,___,___);

С (___,___,___);

D (___,___,___).

А(115,32,45); В(74,4,120); С(25,114,22); D(105,61,110).

А(108,46,50); В(62,13,131); С(15,98,20); D(91,77,124).

А(109,36,46); В(61,13,128); С(11,109,25); D(105,79,105).

А(103,47,48); В(71,10,130); С(25,113,23); D(97,65,115).

А(101,41,41); В(72,5,110); С(21,108,28); D(92,70,100).

А(111,45,37); В(64,8,139); С(12,99,18); D(92,63,120).

А(116,41,36); В(76,6,135); С(20,113,26); D(107,62,125).

А(113,44,40); В(70,2,136); С(18,117,27); D(105,79,120).

А(112,50,40); В(61,2,115); С(15,111,19); D(106,76,115).

А(112,41,47); В(64,13,134); С(18,101,15); D(97,79,128).

А(117,39,47); В(64,2,120); С(12,114,25); D(97,68,120).

А(110,38,49); В(59,11,120); С(19,99,14); D(107,67,85).

А(110,41,47); В(65,1,128); С(11,117,9); D(94,72,136).

А(101,32,50); В(59,2,125); С(21,98,13); D(90,70,120).

А(103,31,49); В(68,3,132); С(17,115,28); D(91,66,115).

А(98,38,35); В(72,5,110); С(22,103,25); D(100,65,100).

А(113,37,35); В(61,14,137); С(29,105,14); D(93,66,120).

А(111,47,50); В(68,13,130); С(14,116,21); D(98,67,127).

А(104,41,35); В(57,0,133); С(13,101,22); D(93,74,125).

А(109,33,38); В(61,5,128); С(13,107,17); D(95,68,120).

А(108,48,44); В(66,5,125); С(26,109,28); D(97,62,120).

А(111,50,52); В(68,1,132); С(15,99,26); D(90,80,120).

А(101,46,41); В(58,2,127); С(17,99,27); D(90,70,110).

А(103,41,48); В(70,8,126); С(18,111,15); D(100,78,120).

А(114,38,49); В(63,14,125); С(16,98,13); D(88,65,115).

А(117,47,37); В(72,3,125); С(24,100,9); D(89,80,120).

А(109,44,35); В(61,12,127); С(29,107,14); D(92,79,120).

28. А(102,36,41); В(73,7,129); С(27,102,17); D(95,67,120).

6 МЕТОД ЗАМІНИ ПЛОЩИН ПРОЕКЦІЙ

1 У чому полягає принцип заміни площин проекцій.

2 Сформулювати алгоритм розв’язання основних задач за допомогою перетворення креслення способом заміни площин проекцій.

Задача 25. Визначити відстань від точки С до прямої АВ. Навести алгоритм розв’язання задачі.

Задача 26. Визначити відстань від точки D до площини Σ (А; В; С). Побудувати точку, симетричну точці D відносно площини. Визначити площу трикутника. Навести алгоритм розв’язання задачі.

Задача 27. Визначити дійсну величину двогранного кута при ребрі ВС.

Задача 28. Знайти відстань між паралельними прямими AB і CD.

7 ТОЧКА ТА ЛІНІЯ НА ПОВЕРХНІ

1 Сформулювати алгоритм побудови на площинах П₁ і П₂ точок та ліній, належних до заданої поверхні.

2 Як визначається видимість лінії на поверхні обертання?

Задача 29. На наведених нижче поверхнях знайти проекції точок та ліній, яких не вистачає. Креслення побудувати в трьох проекціях.

8 ПЕРЕРІЗ ТІЛ ПЛОЩИНОЮ.

ВИЗНАЧЕННЯ НАТУРАЛЬНОЇ ВЕЛИЧИНИ ПЕРЕРІЗУ

1 Які існують методи побудови лінії перерізу багатогранника площиною?
У чому різниця цих методів?

2 Яку фігуру одержуємо при перерізі гранного тіла площиною?

3 Назвати всі можливі види перерізу циліндра та конуса площиною.

4 Що таке опорні точки на лінії перерізу?

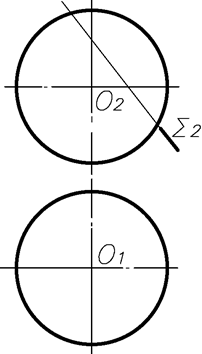
Задача 30. Побудувати дійсну величину перерізів поверхонь площиною Σ.

а) б)

в) г)

Задача 31. Побудувати дійсну величину перерізу а) призми; б) конуса площинами чотирикутника АВСD та трикутника АВС відповідно. Навести алгоритм розв’язання задачі.

а)

Самостійна робота. Побудувати проекції і НВ лінії перетину конуса і піраміди проекціювальною площиною. Виконується на ватмані формату А3 за варіантами індивідуального завдання.

	№ п/п	Розміри (мм)
h	d	а	b	с

9 Перетин прямої з поверхнею

1 Сформулювати алгоритм побудови на площинах П₁ і П₂ точок перетину прямої з поверхнею.

Задача 32. Визначити точки перетину прямої k з поверхнями.

а)

б)

10 АКСОНОМЕТРІЯ

1 Розкрити суть побудови прямокутної ізометрії та симетрії.

2 Як зображати в площинах П₁,П₂, П₃ коло в прямокутних ізометрії та диметрії?

Задача 33. Побудувати ізометрію призми. Знайти проекції вказаних точок в аксонометрії

Задача 34. Побудувати диметрію піраміди. Знайти проекції вказаних точок в аксонометрії.

Задача 35. Побудувати ізометрію конуса. Знайти проекції вказаних точок в аксонометрії.

Задача 36. Побудувати диметрію циліндра. Знайти проекції вказаних точок в аксонометрії.

11 КОМПЛЕКСНЕ КРЕСЛЕННЯ ТІЛ ІЗ КРІЗНИМ ОТВОРОМ

1 Розкрити основні положення державного стандарту «Види, розрізи, перерізи».

Завдання 37. Виконати фронтальний розріз геометричного тіла, суміщений із половиною головного вигляду. Побудувати дійсну величину вказаного похилого перерізу. Побудувати ізометрію з четвертним вирізом.

Завдання 38. Виконати фронтальний розріз геометричного тіла, суміщений із половиною головного вигляду. Побудувати дійсну величину вказаного похилого перерізу. Побудувати диметрію з четвертним вирізом.