 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Линейные преобразования
|
|
Определение: Будем считать, что в линейном пространстве L задано некоторое линейное преобразование А, если любому элементу  Î L по некоторому правилу ставится в соответствие элемент А
Î L по некоторому правилу ставится в соответствие элемент А  Î L.
Î L.
Определение: Преобразование А называется линейным, если для любых векторов  Î L и
Î L и  Î L и любого a верно:
Î L и любого a верно:
A( +
+  ) = A
) = A  +A
+A 
A(a  ) = aA
) = aA 
Определение: Линейное преобразование называется тождественным, если оно преобразует элемент линейного пространства сам в себя.
Е  =
= 
Пример. Является ли А линейным преобразованием. А  =
=  +
+  ;
;  ¹ 0.
¹ 0.
Запишем преобразование А для какого- либо элемента  . А
. А  =
=  +
+ 
Проверим, выполняется ли правило операции сложения для этого преобразования А( +
+  ) =
) =  +
+  +
+  ; A(
; A( ) + A(
) + A( ) =
) =  +
+  +
+  +
+  , что верно только при
, что верно только при  = 0, т.е. данное преобразование А нелинейное.
= 0, т.е. данное преобразование А нелинейное.
Определение: Если в пространстве L имеются векторы линейного преобразования  , то другой вектор
, то другой вектор 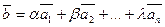 является линейной комбинацией векторов
является линейной комбинацией векторов  .
.
Определение: Если  только при a = b = … = l = 0, то векторы
только при a = b = … = l = 0, то векторы  называются линейно независимыми.
называются линейно независимыми.
Определение: Если в линейном пространстве L есть n линейно независимых векторов и любые n + 1 векторов линейно зависимы, то пространство L называется n-мерным, а совокупность линейно независимых векторов называется базисом линейного пространства L.
Следствие: Любой вектор линейного пространства может быть представлен в виде линейной комбинации векторов базиса.
Пусть в n- мерном линейном пространстве с базисом 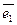 ,
,  ,…,
,…,  задано линейное преобразование А. Тогда векторы А
задано линейное преобразование А. Тогда векторы А 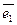 ,А
,А  ,…,А
,…,А  - также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:
- также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:
A 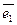 = a11
= a11 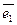 + a21
+ a21  +…+ an1
+…+ an1 
A  = a12
= a12 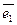 + a22
+ a22  +…+ an2
+…+ an2 
……………………………….
A  = an1
= an1 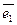 + an2
+ an2  +…+ ann
+…+ ann 
Тогда матрица А =  называется матрицей линейного преобразования А.
называется матрицей линейного преобразования А.
Если в пространстве L взять вектор  = x1
= x1 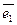 + x2
+ x2  +…+ xn
+…+ xn  , то A
, то A  Î L.
Î L.
 , где
, где
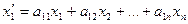
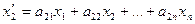
……………………………..

Эти равенства можно назвать линейным преобразованием в базисе 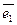 ,
,  ,…,
,…,  .
.
В матричном виде:
 , А×
, А×  ,
, 
Пример. Найти матрицу линейного преобразования, заданного в виде:
x¢ = x + y
y¢ = y + z
z¢ = z + x
x¢ = 1×x + 1×y + 0×z
y¢ = 0×x + 1×y + 1×z
z¢ = 1×x + 0×y + 1×z
A = 
На практике действия над линейными преобразованиями сводятся к действиям над их матрицами.
Определение: Если вектор  переводится в вектор
переводится в вектор  линейным преобразованием с матрицей А, а вектор
линейным преобразованием с матрицей А, а вектор  в вектор
в вектор  линейным преобразованием с матрицей В, то последовательное применение этих преобразований равносильно линейному преобразованию, переводящему вектор
линейным преобразованием с матрицей В, то последовательное применение этих преобразований равносильно линейному преобразованию, переводящему вектор  в вектор
в вектор  (оно называется произведением составляющих преобразований).
(оно называется произведением составляющих преобразований).
С = В×А
Пример. Задано линейное преобразование А, переводящее вектор  в вектор
в вектор  и линейное преобразование В, переводящее вектор
и линейное преобразование В, переводящее вектор  в вектор
в вектор  . Найти матрицу линейного преобразования, переводящего вектор
. Найти матрицу линейного преобразования, переводящего вектор  в вектор
в вектор  .
.



С = В×А

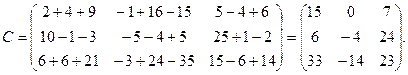
Т.е. 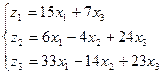
Примечание: Если ïАï= 0, то преобразование вырожденное, т.е., например, плоскость преобразуется не в целую плоскость, а в прямую.
Дата публикования: 2015-11-01; Прочитано: 269 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
