Раздел 2.4 Функции многих переменных

Задание 2.4.1

Найти все частные производные второго порядка функции и значение указанной частной производной в указанной точке.

Вариант 1 , .

Вариант 2 , .

Вариант 3 , .

Вариант 4 , .

Вариант 5 , .

Вариант 6 , .

Вариант 7 , .

Вариант 8 , .

Вариант 9 , .

Вариант 10 , .

Задание 2.4.2

Даны: скалярное поле , точки и .

Найти:

а) градиент поля в точке ;

б) производную функции в точке по направлению от точки к точке .

Вариант 1 , , .

Вариант 2 , , .

Вариант 3 , , .

Вариант 4 , , .

Вариант 5 , , .

Вариант 6 , , .

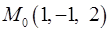Вариант 7 , , .

Вариант 8 , , .

Вариант 9, , , .

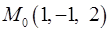Вариант 10 , , .

Задание 2.4.3

Разложить функцию 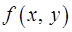по формуле Тейлора второго порядка в окрестности точки .

Пользуясь этой формулой, найти приближенное значение функции в точке .

Вариант 1 , , .

Вариант 2 , , .

Вариант 3 , , .

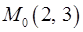Вариант 4 , , .

Вариант 5 , , .

Вариант 6 , , .

Вариант 7 , , .

Вариант 8 , , .

Вариант 9 , , .

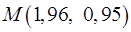Вариант 10 , , .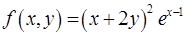

Задание 2.4.4

Найти функции , заданной неявно уравнением .

Вариант 1 .

Вариант 2 .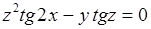

Вариант 3 .

Вариант 4 .

Вариант 5 .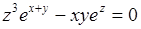

Вариант 6 .

Вариант 7 .

Вариант 8 .

Вариант 9 .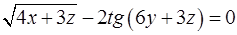

Вариант 10 .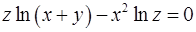

Задание 2.4.5

Найти точки экстремума функции и определить их характер.

Вариант 1 .

Вариант 2 .

Вариант 3 .

Вариант 4 .

Вариант 5 .

Вариант 6 .

Вариант 7 .

Вариант 8 .

Вариант 9 .

Вариант 10 .

Задание 2.4.6

Найти и в замкнутой области D, заданной системой неравенств. Сделать рисунок области D.

Вариант 1 .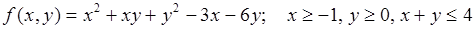

Вариант 2 .

Вариант 3 .

Вариант 4 .

Вариант 5 .

Вариант 6 .

Вариант 7 .

Вариант 8 .

Вариант 9 .

Вариант 10 .