Решение ур-я Шредингера для атома водорода. Полная система квантовых чисел. Принцип Паули

Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze (для атома водорода Z = 1),

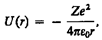(223.1)

где r — расстояние между электроном и ядром. Графически функция U (r) изображена жирной кривой на рис. 302. U (r) с уменьшением r (при приближении электрона к ядру) неограниченно убывает.

Состояние электрона в атоме водорода описывается волновой функцией y, удовлетворяющей стационарному уравнению Шредингера (217.5), учитывающему значение (223.1):

(223.2)

где т — масса электрона, Е — полная энергия электрона в атоме. Так как поле, в котором движется электрон, является центрально-симметричным, то для решения уравнения (223.2) обычно используют сферическую систему координат: r, q, j. Не вдаваясь в математическое решение этой задачи, ограничимся рассмотрением важней­ших результатов, которые из него следуют, пояснив их физический смысл.

1. Энергия. В теории дифференциальных уравнений доказывается, что уравнения типа (223.2) имеют решения, удовлетворяющие требованиям однозначности, конеч­ности и непрерывности волновой функции y, только при собственных значениях энергии

(223.3)

т. е. для дискретного набора отрицательных значений энергии.

Энергия ионизации атома водорода равна

2. Квантовые числа. В квантовой механике доказывается, что уравнению Шредингера (223.2) удовлетворяют собственные функции , определяемые тремя квантовыми числами: главным п, орбитальным l и магнитным т_l.

Главное квантовое число n, согласно (223.3), определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения начиная с еди­ницы:

Из решения уравнения Шредингера вытекает, что момент импульса (механический орбитальный момент) электрона квантуется, т. е. не может быть произвольным, а принимает дискретные значения, определяемые формулой

(223.4)

где l — орбитальное квантовое число, которое при заданном n принимает значения

(223.5)

т. е. всего n значений, и определяет момент импульса электрона в атоме.

Из решения уравнений Шредингера следует также, что вектор L _l момента импульсаэлектрона может иметь лишь такие ориентации в пространстве, при которых его проекция L_lx на направление z внешнего магнитного поля принимает квантованныезначения, кратные ћ:

(223.6)

где т_l— магнитное квантовое число, которое при заданном l может принимать значения

(223.7)

т. е. всего 2 l +1 значений. Таким образом, магнитное квантовое число m_l определяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2 l +1 ориентации.

Если тождественные частицы имеют одинаковые квантовые числа, то их волновая функция симметрична относительно перестановки частиц. Отсюда следует, что два одинаковых фермиона, входящих в одну систему, не могут находиться в одинаковых состояниях, так как для фермионов волновая функция должна быть антисимметрич­ной. Обобщая опытные данные, В. Паули сформулировал принцип, согласно которому системы фермионов встречаются в природе только в состояниях, описываемых ан­тисимметричными волновыми функциями (квантово-механическая формулировка принципа Паули).

Из этого положения вытекает более простая формулировка принципа Паули, которая и была введена им в квантовую теорию (1925) еще до построения квантовой механики: в системе одинаковых фермионов любые два из них не могут одновременно находиться в одном и том же состоянии. Отметим, что число однотипных бозонов, находящихся в одном и том же состоянии, не лимитируется.

Напомним, что состояние электрона в атоме однозначно определяется набором четырех квантовых чисел:

Распределение электронов в атоме подчиняется принципу Паули, который может быть использован в его простейшей формулировке: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел п, l, m_l и т_s т. е.

где Z (п, l, m_l, т_s) — число электронов, находящихся в квантовом состоянии, описыва­емом набором четырех квантовых чисел: п, l, m_l, т_s. Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме, различаются значениями по крайней мере одного квантового числа.

Согласно формуле (223.8), данному n соответствует n ² различных состояний, от­личающихся значениями l и m_l. Квантовое число т_s может принимать лишь двазначения (± ½). Поэтому максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом, равно

Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой. В каждой из оболочекэлектроны распределяются по подоболочкам, соответствующим данному l. Поскольку орбитальное квантовое число принимает значения от 0 до n –1, число подоболочек равно порядковому номеру n оболочки. Количество электронов в подоболочке опреде­ляется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочкес данным l равно 2(2 l +1). Обозначения оболочек, а также распределение электронов по оболочкам и подоболочкам представлены в табл. 6.

Таблица 6