Волновое уравнение для электромагнитного поля. Свойства электромагнитных волн. Энергия электромагнитных волн. Вектор Пойнтинга. Излучение диполя

Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением — дифференциальным уравнением в частных производных

или

(154.9)

где v — фазовая скорость, — оператор Лапласа. Решением урав­нения (154.9) является уравнение любой волны. Соответствующей подстановкой можно убедиться, что уравнению (154.9) удовлетворяют, в частности, плоская волна (см. (154.2)) и сферическая волна (см. (154.7)). Для плоской волны, распространяющейся вдоль оси х, волновое уравнение имеет вид

Электромагнитная волна - распространение электромагнитных полей в пространстве и во времени.

Источник электромагнитного поля - электрические заряды, движущиеся с ускорением.

Электромагнитные волны, в отличие от упругих (звуковых) волн, могут распространяться в вакууме или любом другом веществе.

Электромагнитные волны в вакууме распространяются со скоростью c=299 792 км/с, то есть со скоростью света.

В веществе скорость электромагнитной волны меньше, чем в вакууме. Соотношение междудлиной волна, ее скоростью, периодом и частотой колебаний, полученные для механических волн выполняются и для электромагнитных волн:

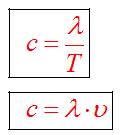
Колебания вектора напряженности E и вектора магнитной индукции B происходят во взаимно перпендикулярных плоскостях и перпендикулярно направлению распространения волны (вектору скорости).

Электромагнитная волна переносит энергию.

Возможность обнаружения электромагнитных воли указывает на то, что они переносят энергию. Объемная плотность w энергии электромагнитной волны складывается из объемных плотностей w _эл (см. (95.8)) и w _м, (см. (130.3)) электрического и магнитного полей:

Учитывая выражение (162.4), получим, что плотности энергии электрического и маг­нитного полей в каждый момент времени одинаковы, т. е. w _эл = w _м. Поэтому

Умножив плотность энергии w на скорость v распространения волны в среде (см. (162.3)), получим модуль плотности потока энергии:

Tax как векторы Е и Н взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора [ ЕН ] совпада­ет с направлением переноса энергии, а модуль этого вектора равен ЕН. Вектор плотности потока электромагнитной энергии называется вектором Умова — Пойнтинга:

Вектор S направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.

Простейшим излучателем электромагнитных волн является электрический диполь, электрический момент которого изменяется во времени по гармоническому закону

где р ₀ — амплитуда вектора р. Примером подобного диполя может служить система, состоящая из покоящегося положительного заряда + Q и отрицательного заряда –Q, гармонически колеблющегося вдоль направления р с частотой w.

Если волна распространяется в однородной изотропной среде, то время прохожде­ния волны до точек, удаленных от диполя на расстояние r, одинаково. Поэтому во всех точках сферы, центр которой совпадает с диполем, фаза колебаний одинакова, т. е. в волновой зоне волновой фронт будет сферическим и, следовательно, волна, излуча­емая диполем, есть сферическая волна.

В каждой точке векторы Е и Н колеблются по законуcos(wt—kr), амплитуды этих векторов пропорциональны (1/ r) sin q (для вакуума), т. е. зависят от расстояния r до излучателя и угла q между направлением радиуса-вектора и осью диполя. Отсюда следует, что интенсивность излучения диполя в волновой зоне

(164.1)

Зависимость (164.1) I от q при заданном значении r, приводимая в полярных коор­динатах (рис. 228), называется диаграммой направленности излучения диполя. Как видно из выражения (164.1) и приведенной диаграммы, диполь сильнее всего излучает в на­правлениях, перпендикулярных его оси (q = p /2). Вдоль своей оси (q =0 и q = p) диполь не излучает вообще. Диаграмма направленности излучения диполя позволяет фор­мировать излучение с определенными характеристиками и используется при констру­ировании антенн.