Дифференциальное уравнение гк. Гармонические осцилляторы: маятники, груз на пружине, колебательный контур. Энергетические соотношения для осцилляторов

Гармонические колеба­ния величины s описываются уравнением типа

(140.1)

где А — максимальное значение колеблющейся величины, называемое амплитудой колебания, w ₀ — круговая (циклическая) частота, j — начальная фаза колебания в мо­мент времени t= 0, (w ₀ t + j) — фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до –1, то s может принимать значения от +А до –А.

Определенные состояния системы, совершающей гармонические колебания, повто­ряются через промежуток времени Т, называемый периодом колебания, за которыйфаза колебания получает приращение 2 p, т. е.

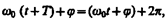
откуда

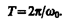(140.2)

Величина, обратная периоду колебаний,

(140.3)

т. е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (140.2) и (140.3), получим

Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, при кото­рой за 1 с совершается один цикл процесса.

Запишем первую и вторую производные по времени от гармонически колеблющей­ся величины s:

(140.4)

(140.5)

т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (140.4) и (140.5) соответственно равны Аw ₀ и Аw . Из выражения (140.5) следует дифференциальное уравнение гармонических колебаний

(140.6)

(где s = A cos (w ₀ t + j)). Решением этого уравнения является выражение (140.1).

Гармоническим осциллятором называется система, совершающая колебания, описыва­емые уравнением вида (140.6);

(142.1)

Колебания гармонического осциллятора являются важным примером периодического движения и служат точной или приближенной моделью во многих задачах классичес­кой и квантовой физики. Примерами гармонического осциллятора являются пружин­ный, физический и математический маятники, колебательный контур (для токов и на­пряжений столь малых, что элементы контура можно было бы считать линейными; см. §146).

1. Пружинный маятник — это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника

Из выражений (142.1) и (140.1) следует, что пружинный маятник совершает гармоничес­кие колебания по закону х=А соs (w₀ t + j) с циклической частотой

(142.2)

и периодом

(142.3)

Формула (142.3) справедлива для упругих колебаний в пределах, в которых выполняет­ся закон Гука (см. (21.3)), т. е. когда масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, согласно (141.5) и (142.2), равна

2. Физический маятник — это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс С тела (рис. 201).

Если маятник отклонен из положения равновесия на некоторый угол a, то в соот­ветствии с уравнением динамики вращательного движения твердого тела (18.3) момент M возвращающей силы можно записать в виде

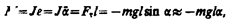(142.4)

где J — момент инерции маятника относительно оси, проходящей через точку подве­са О, l – расстояние между ней и центром масс маятника, F_t= –mgsina» –mga. — возвращающая сила (знак минус обусловлен тем, что направления F_t и a всегда противоположны;sin a» a соответствует малым колебаниям маятника,т.е. малым отклонениям маятника из положения равновесия). Уравнение (142.4) можно записать в виде

Принимая

(142.5)

получим уравнение

идентичное с (142.1), решение которого (140.1) известно:

(142.6)

Из выражения (142.6) следует, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой w₀ (см. (142.5)) и периодом

(142.7)

где L=J/ (ml) — приведенная длина физического маятника.

Точка О' на продолжении прямой ОС, отстоящая от точки О подвеса маятника на расстоянии приведенной длины L, называется центром качаний физического маятника (рис. 201). Применяя теорему Штейнера (16.1), получим

т. е. ОО' всегда больше ОС. Точка подвеса О маятника и центр качаний О' обладают свойством взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О подвеса

станет новым центром качаний, и период колебаний физичес­кого маятника не изменится.

3. Математический маятник — это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой невесомой нити, и колеб­лющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити. Момент инерции математического маятника

(142.8)

где l — длина маятника.

Так как математический маятник можно представить как частный случай физичес­кого маятника, предположив, что вся его масса сосредоточена в одной точке — центре масс, то, подставив выражение (142.8) в формулу (1417), получим выражение для периода малых колебаний математического маятника

(142.9)

Сравнивая формулы (142.7) и (142.9), видим, что если приведенная длина L физичес­кого маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Следовательно, приведенная длина физического маятника — это длина такого математического маятника, период колебаний которого совпадает с пери­одом колебаний данного физического маятника.