 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема Гюйгенса
|
|
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
Доказательство
Вычислим приведенную длину для нового маятника:
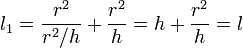 .
.
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания.
Для этого умножим левую  и правую часть этого уравнения на
и правую часть этого уравнения на  . Тогда:
. Тогда:  .
.
Интегрируя это уравнение, получаем 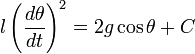 , где
, где 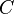 произвольная постоянная. Её можно найти из граничного условия, что в моменты
произвольная постоянная. Её можно найти из граничного условия, что в моменты  .
.
Получаем:  .
.
Подставляем и преобразовываем получившееся уравнение: 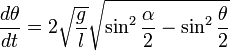 .
.
Отделяем переменные и интегрируем это уравнение: 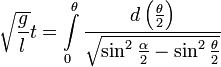 .
.
Удобно сделать замену переменной, полагая 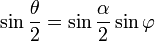 . Тогда искомое уравнение принимает вид:
. Тогда искомое уравнение принимает вид:
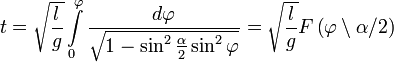 .
.
Здесь 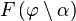 — нормальный эллиптический интеграл Лежандра 1-го рода. Для периода колебаний получаем формулу:
— нормальный эллиптический интеграл Лежандра 1-го рода. Для периода колебаний получаем формулу:
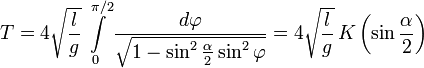 .
.
Здесь 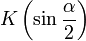 — полный нормальный эллиптический интеграл Лежандра 1-го рода. Раскладывая его в ряд, можно получить удобную для практических вычислений формулу:
— полный нормальный эллиптический интеграл Лежандра 1-го рода. Раскладывая его в ряд, можно получить удобную для практических вычислений формулу:
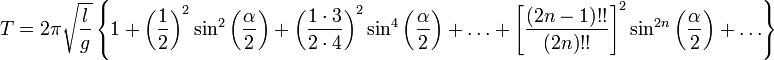 .
.
Дата публикования: 2015-11-01; Прочитано: 401 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
