 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Основной закон динамики вращательного движения твердого тела
|
|
Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела
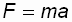 , где
, где 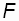 – сила, приложенная к телу массой m; а – линейное ускорение тела.
– сила, приложенная к телу массой m; а – линейное ускорение тела.
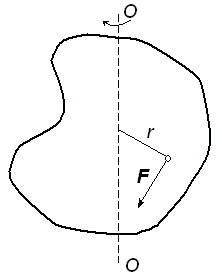 Если к твердому телу массой m в точке А приложить силу
Если к твердому телу массой m в точке А приложить силу 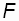 , то в результате жесткой связи между всеми материальными точками тела все они получат угловое ускорение
, то в результате жесткой связи между всеми материальными точками тела все они получат угловое ускорение 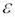 и соответственные линейные ускорения, как если бы на каждую точку действовала сила
и соответственные линейные ускорения, как если бы на каждую точку действовала сила 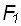 ,…,
,…, 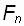 . Для каждой материальной точки можно записать:
. Для каждой материальной точки можно записать:
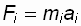 , где
, где 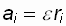 , поэтому
, поэтому 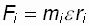 ,
,
Умножая левую и правую части уравнения (1.7) на ri, получают
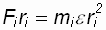 , (1.8) где
, (1.8) где 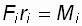 – момент силы – это произведение силы
– момент силы – это произведение силы 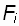 на ее плечо ri.
на ее плечо ri.
Плечом силы называют кратчайшее расстояние от оси вращения “ОО” (рис. 5) до линии действия силы 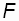 .
.
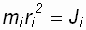 – момент инерции i -й материальной точки.
– момент инерции i -й материальной точки.
Выражение (1.8) можно записать так: 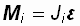 . (1.9)
. (1.9)
Просуммируем левую и правую части (1.9) по всем точкам тела: 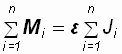 .
.
Обозначим 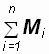 через М, а
через М, а 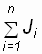 через J, тогда
через J, тогда 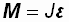 (1.10)
(1.10)
Уравнение (1.10) – основной закон динамики вращательного движения твердого тела. Величина 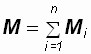 – геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорение
– геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорение 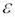 .
. 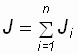 – алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: “Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение”.
– алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: “Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение”.
Мгновенное значение углового ускорения 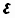 , есть первая производная угловой скорости
, есть первая производная угловой скорости 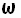 по времени t, то есть
по времени t, то есть 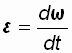 , (1.11) где
, (1.11) где 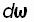 – элементарное изменение угловой скорости тела за элементарный промежуток времени dt.
– элементарное изменение угловой скорости тела за элементарный промежуток времени dt.
Если в выражение основного закона (1.10) поставить значение мгновенного ускорения (1.11), то
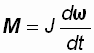 или
или 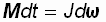 , где
, где 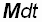 – импульс момента силы – это произведение момента силы М на промежуток времени dt.
– импульс момента силы – это произведение момента силы М на промежуток времени dt.
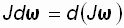 – изменение момента импульса тела,
– изменение момента импульса тела,
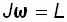 – момент импульса тела есть произведение момента инерции J на угловую скорость
– момент импульса тела есть произведение момента инерции J на угловую скорость 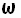 , а
, а 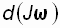 есть d L.
есть d L.
Поэтому основной закон динамики вращательного движения твердого тела формулируется так: “Импульс момента силы 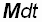 , действующий на вращательное тело, равен изменению его момента импульса d L ”:
, действующий на вращательное тело, равен изменению его момента импульса d L ”:
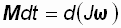 или
или 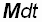 = d L.
= d L.
12. Основные понятия: момент силы, момент импульса, момент инерции.
Для характеристики вращательного эффекта силы при действии ее на твердое тело вводят понятие момента силы. Различают моменты силы относительно неподвижной точки и относительно неподвижной оси.
Моментом силы относительно неподвижной точки О называется физическая величина М, определяемая векторным произведением радиуса-вектора г, проведенного из точки О в точку Л приложения силы, на силу F:
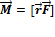 , где
, где 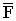 - равнодействующая всех сил, действующих на материальную точку.
- равнодействующая всех сил, действующих на материальную точку.
Равнодействующая сила – это сила, которая равна результирующей 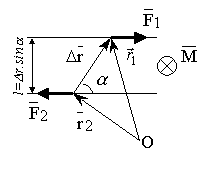 силе
силе  и которая создает момент, равный суммарному моменту всех внешних сил.
и которая создает момент, равный суммарному моменту всех внешних сил.
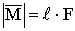 - модуль момента,
- модуль момента,
где 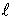 - плечо вектора
- плечо вектора 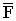 относительно точки О.
относительно точки О.
Пара сил – это две равные по модулю, противоположено направленные и не действующие вдоль одной прямой силы 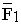 и
и 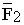 .
.
Плечо пары – расстояние 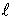 между прямыми, вдоль которых действуют силы.
между прямыми, вдоль которых действуют силы.
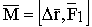 - момент пары относительно любой точки одинаков.
- момент пары относительно любой точки одинаков.
При изучении вращения твердых тел пользуются понятием момента инерции. Момент инерции тела — мера инертности твердых тел при вращательном движении. Его роль такая же, что и массы при поступательном движении. Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс п материальных точек системы на квадраты их расстоянии до рассматриваемой оси:
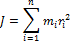
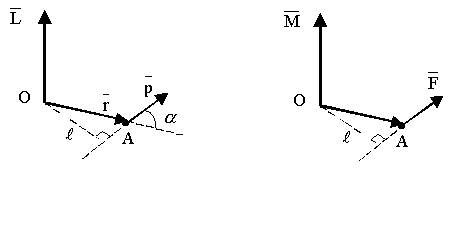 Моментом импульса материальной точки относительно некоторой точки О выбранной системы отсчета называется вектор
Моментом импульса материальной точки относительно некоторой точки О выбранной системы отсчета называется вектор 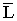 равный векторному произведению векторов
равный векторному произведению векторов 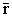 и
и 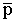 :
:
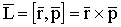 ,
,
где 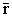 - радиус-вектор материальной точки относительно точки О.
- радиус-вектор материальной точки относительно точки О.
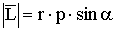 - модуль вектора момента импульса,
- модуль вектора момента импульса,
где 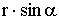 - плечо вектора
- плечо вектора 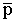 относительно точки О.
относительно точки О.
13. Момент инерции и теорема Штейнера.
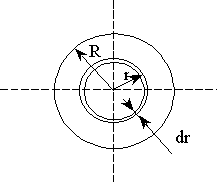
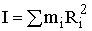 - момент инерции твердого тела относительно оси, где
- момент инерции твердого тела относительно оси, где 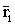 - радиус-вектор
- радиус-вектор 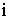 -ой частицы,
-ой частицы, 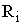 - расстояние от оси вращения до
- расстояние от оси вращения до 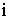 -ой частицы.
-ой частицы.
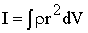 - формула для определения момента инерции твердого тела, где
- формула для определения момента инерции твердого тела, где 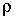 - плотность тела в данной точке,
- плотность тела в данной точке, 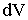 - объем элемента, находящегося на расстоянии
- объем элемента, находящегося на расстоянии 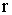 от оси
от оси 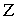 .
.
Моменты инерции некоторых однородных тел массой 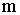
| Тело | 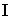
| |
| Обруч (кольцо) | 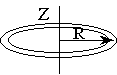
| 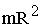
|
| Тонкий стержень: 1. относительно середины 2. относительно конца | 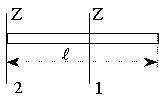
| 1. 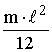 2.
2. 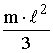
|
| Диск (цилиндр): 1. относительно центра 2. относительно образующей | 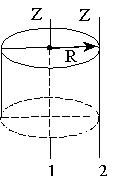
| 1. 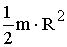 2.
2. 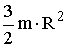
|
| 1. Шар 2. Сферическая оболочка | 
| 1. 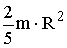 2.
2. 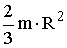
|
Теорема Штейнера:
момент инерции 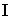 относительно произвольной оси равен сумме момента инерции
относительно произвольной оси равен сумме момента инерции 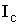 относительно оси, параллельной данной, и проходящей через центр масс
относительно оси, параллельной данной, и проходящей через центр масс 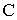 тела, и произведения массы тела на квадрат расстояния
тела, и произведения массы тела на квадрат расстояния 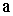 между осями
между осями 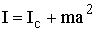 .
.
Дата публикования: 2015-11-01; Прочитано: 49936 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
