 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вычисление относительной скорости
|
|
| X |
| Y |
| Z |
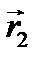
|
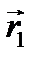
|
| R |
| m2 |
| m1 |
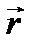
|
| Система координат |
 - относительной скорости двух молекул, движущихся со скоростями
- относительной скорости двух молекул, движущихся со скоростями 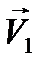 и
и 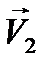 . Эту задачу удобнее решать в системе центра масс.
. Эту задачу удобнее решать в системе центра масс.
Обозначим m1 и m2 массы молекул первого и второго сорта газа, 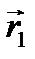 и
и 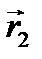 – радиусы-векторы первой и второй молекул.
– радиусы-векторы первой и второй молекул. 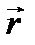 – расстояние между молекулами, R – радиус-вектор центра масс (рисунок).
– расстояние между молекулами, R – радиус-вектор центра масс (рисунок).
Тогда в выбранной системе координат
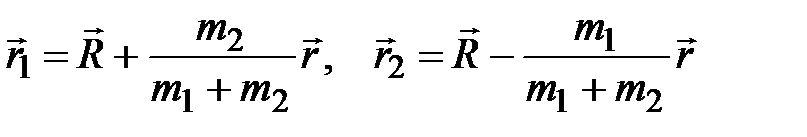 . .
| (1) |
Дифференцируя эти равенства, получим
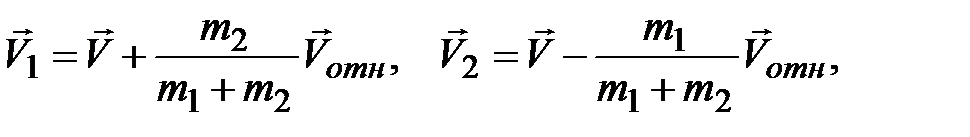
| (2) |
Здесь 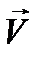 – скорость центра масс системы двух частиц,
– скорость центра масс системы двух частиц,  – относительная скорость этих молекул. Как видно из выражения (2), преобразование линейное и Якобиан преобразования
– относительная скорость этих молекул. Как видно из выражения (2), преобразование линейное и Якобиан преобразования 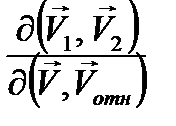 =1 (доказать), следовательно,
=1 (доказать), следовательно,
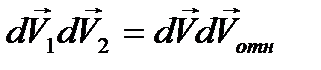 . .
| (3) |
С учетом теоремы умножения вероятности независимых событий, функция распределения молекул по скоростям есть произведение функций Максвелла
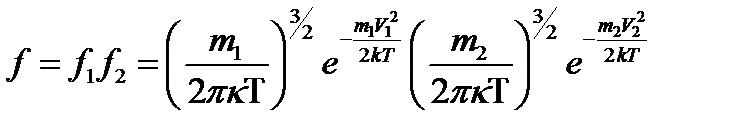 . .
| (4) |
Соответственно в новых координатах (2) показатель степени запишется:
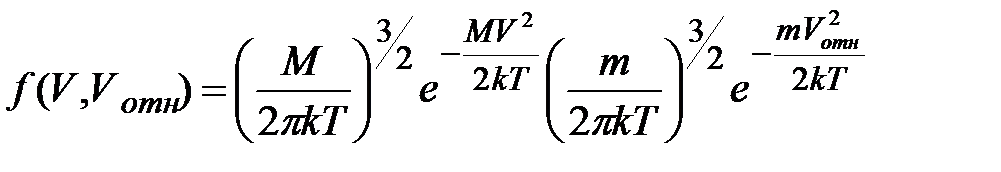
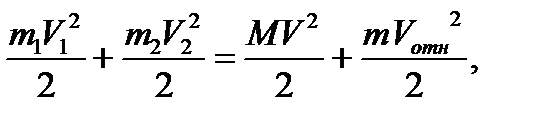 где
где 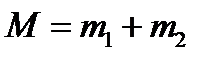 – масса системы;
– масса системы; 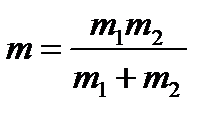 – приведенная масса.
– приведенная масса.
Таким образом, вероятность того, что система двух частиц имеет скорость в «объеме» пространства скоростей 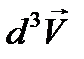 и
и 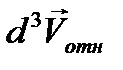 равна
равна
 .
.
Очевидно, что
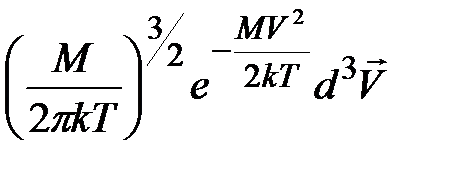 – вероятность для скорости всей системы, а
– вероятность для скорости всей системы, а
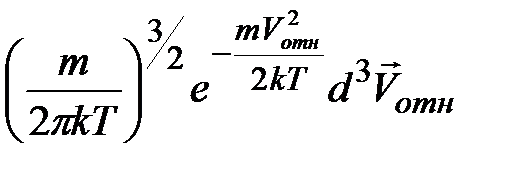 – вероятность для относительной скорости молекул.
– вероятность для относительной скорости молекул.
Тогда искомая средняя относительная скорость равна
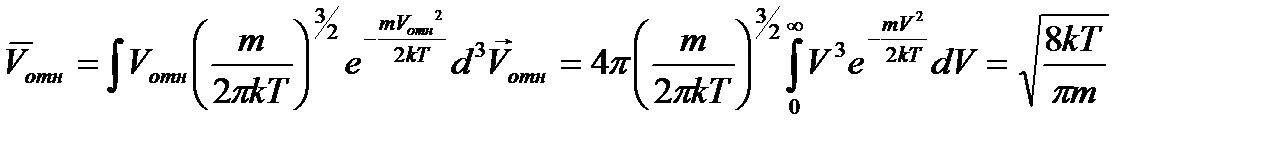 .
.
В случае молекул с одинаковыми массами (m 1 = m 2 и 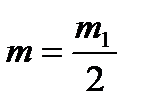 )
)
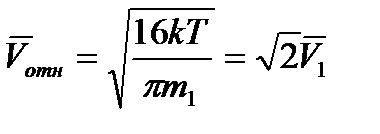 .
.
Приложение 2
Вывод формулы для оценки значения 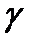
Ранее были введены обозначения 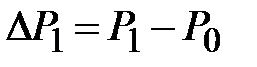 и
и  , причем
, причем 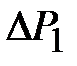 и
и  (см. рис.2). Запишем уравнение для адиабатического расширения газа (кривая 3-4)
(см. рис.2). Запишем уравнение для адиабатического расширения газа (кривая 3-4)
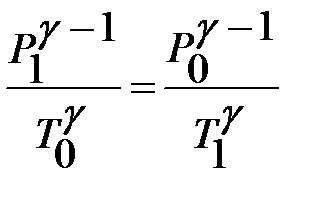 или
или  .
.
Воспользовавшись формулой бинома Ньютона и ограничиваясь двумя членами, получим
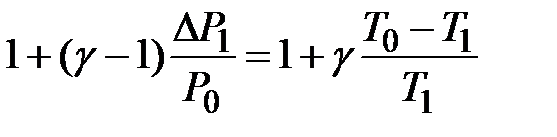 ;
; 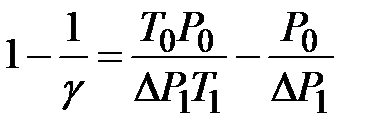 .
.
Учитывая, что 4 и 5 лежат на одной изохоре, т.е. 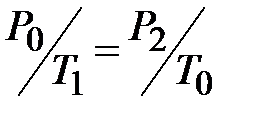 , можно записать:
, можно записать:
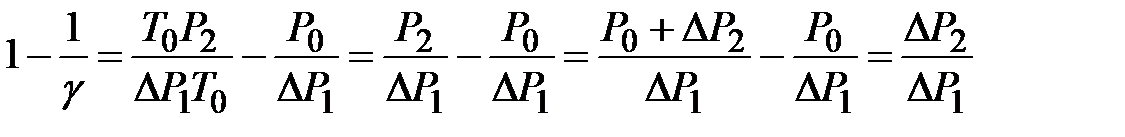 .
.
Откуда
 . .
|
Дата публикования: 2015-11-01; Прочитано: 553 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
