Математическое ожидание

Среднее арифметическое, являющееся центром эмпирического распределения, переходит в математическое ожидание M(x) при . В теоретическом распределении дискретных величин математическое ожидание

.

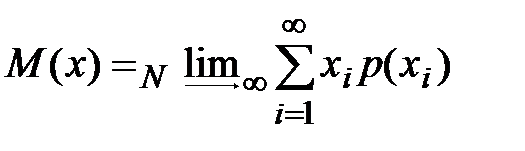(2-1.20)

Математическое ожидание непрерывно распределенной величины

.

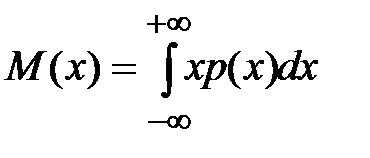(2-1.21)

При многократных экспериментальных определениях некоторой величины в одних и тех же условиях (при отсутствии систематических погрешностей) математическое ожидание можно рассматривать как "истинное" значение этой величины.

Дисперсия

В теоретическом распределении дисперсия есть математическое ожидание квадрата отклонений случайной величины от её математического ожидания

.

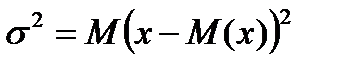(2-1.22)

Если обозначить M(x) = a, то дисперсия распределения дискретной величины может быть записана как

,

(2-1.23)

в случае непрерывной величины как

.

(2-1.24)