Деление и построение углов

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

Наиболее простыми геометрическими построениями на чертежах являются: деление отрезков прямой и углов на равные части; деление окружности на равные части; построение уклонов и конусности; различные виды сопряжения прямых с дугами окружности и дуг окружности между собой. Рассмотрим основные приемы выполнения геометрических построений на чертежах.

Деление отрезка прямой на равные части

Деление отрезка прямой на две или четыре равные части. Деление отрезка на две равные части (рис. 1.9, а) выполняют в следующей последовательности: из концов отрезка АВ радиусом R, чуть большим половины отрезка, делают засечки до их взаимного пересечения выше и ниже отрезка АВ\ полученные точки пересечения соединяют прямой KL. Прямая, соединяющая точки К и L, делит отрезок АВ на две равные части: АС и СВ.

Если отрезок АВ необходимо разделить на четыре равные части, то подобные построения повторяют для отрезков АС и СВ. При этом радиус r должен быть больше половины отрезка СВ.

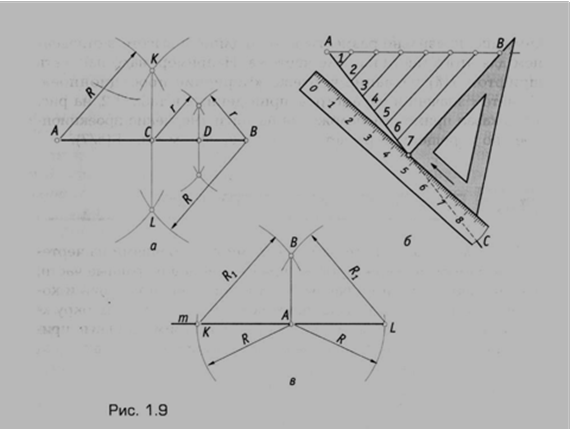
Деление отрезка на любое число равных частей. Пусть отре­зок АВ требуется разделить на семь равных частей. Из точки А (рис. 1.9, б) проводят вспомогательную прямую АС под любым острым углом. На этой прямой от точки А откладывают семь равных отрезков произвольной длины; полученную точку 7 соединяют с точкой В — концом заданного отрезка. Из точек деления на вспомогательной прямой АС, используя линейку и угольник, проводят прямые, параллельные прямой 7В, которые разделят отрезок АВ на семь равных частей.

Построение перпендикуляра к прямой в заданной на ней точке. Чтобы построить перпендикуляр к прямой, необходимо на за­данной прямой m (рис. 1.9, в) по обе стороны от точки А сделать засечки радиусом R произвольного размера. Затем из полученных точек К и L нужно сделать циркулем засечки радиусом R₁, немного большим, чем радиус R. Точку А соединяют прямой с точкой В — точкой пересечения засечек. Полученная прямая АВ перпендикулярна прямой m.

Деление и построение углов

Деление угла на две равные части. Из вершины угла — точки А (рис. 1.10, а) проводят дугу произвольного радиуса R до пересечения со сторонами АВ и АС в точках М и N. Из этих точек проводят дуги радиусом R₁ большим половины длины дуги MN, до их пересечения в точке К. Соединяя вершину угла А с точкой К, получают биссектрису угла АК.

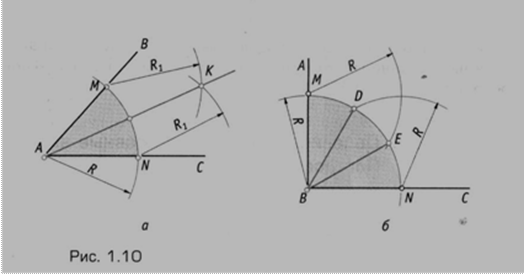
Деление прямого угла на три равные части. Чтобы разделить прямой угол на три равные части (рис. 1.10, б), из вершины В произвольным радиусом R проводят дугу до пересечения со сто­ронами прямого угла АВ и ВС в точках М и N. Из точек М и N проводят дуги того же радиуса до пересечения с дугой MN. По­лученные точки Е и D соединяют прямыми с вершиной угла В. Прямые BE и BD разделят прямой угол на три равные части, каж­дый угол которой равен 30°.