Кусочно–линейная интерполяция

На каждом интервале 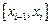функция является линейной . Значения коэффициентов находятся из выполнения условий интерполяции в концах отрезка:

Получаем систему уравнений:

,

откуда находим . Следовательно, функцию можно записать в виде:

,

то есть

Или При использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение 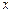, а затем подставить его в формулу. Итоговая функция будет непрерывной, но производная будет разрывной в каждом узле интерполяции. Погрешность такой интерполяции будет меньше, чем в случае кусочно–постоянной интерполяции.

Пример. Заданы значений некоторой функции:

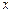
				3,5
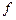
	-1	0,2	0,5	0,8

Требуется найти значение функции при и по кусочно–постоянной и кусочно–линейной интерполяции.

Решение. Точка принадлежит первому локальному отрезку , то есть 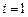и, следовательно, по формулам левой кусочно–постоянной интерполяции , по формулам правой кусочно–постоянной интерполяции . Воспользуемся формулами кусочно–линейной интерполяции: