Виды дисперсий и правило их сложения

Разделив изучаемую совокупность на качественно однородные группы, можно исчислить для каждой из групп среднюю и дисперсию.

Групповая средняя говорит о среднем размере изучаемого признака данной группы единиц.

Групповая дисперсия характеризует средний квадрат отклонения индивидуальных значений данного признака от групповой средней.

Рассчитаем эти показатели по следующим данным:

Задача.

Урожайность картофеля по участкам

Урожайность, в ц с 1 га	Участки, га
Всего	в том числе
удобренные	неудобренные
до 100		–
100-120
120-140
140 и выше			–
Итого

Определим групповые средние по формуле:

,

где – численность вариант в каждой группе.

Средняя урожайность картофеля на удобренных участках:

ц.

Средняя урожайность на неудобренных участках:

ц.

Исчислим групповые дисперсии:

.

Дисперсия урожайности на удобренных участках:

Дисперсия урожайности на неудобренных участках:

Можно рассматривать всю совокупность как единое целое, не подразделяя ее на группы и тоже исчислить общую среднюю и общую дисперсию.

Общая средняя характеризует средний размер признака в данной совокупности в целом.

Общая дисперсия показывает средний квадрат отклонений индивидуальных значений от общей (генеральной) средней.

Рассчитаем общую среднюю по формуле:

где – численность всей совокупности.

ц.

Общая дисперсия: .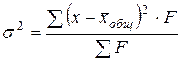

Между групповой и общей средней можно исчислить показатель вариации, где групповые средние рассматриваются как индивидуальные значения совокупности, это межгрупповая дисперсия:

Межгрупповая дисперсия служит мерой колеблемости частных (групповых) средних около общей средней. Величина межгрупповой дисперсии указывает насколько частные совокупности однороднее общей.

Таким образом получается три вида дисперсий: общая, групповая и межгрупповая. Все эти дисперсии взаимосвязаны между собой следующим образом: величина общей дисперсии равна сумме межгрупповой дисперсии и средней дисперсии из групповых.

Средняя дисперсия из групповых вычисляется как средняя взвешенная величина, в качестве веса берется численность каждой группы ():

Проверим взаимосвязь дисперсий, которую в математике называют теоремой или правилом сложения дисперсий:

Общая дисперсия отражает вариацию результативного признака, вызванную воздействием всей совокупности факторов. В нашем примере она показывает вариацию урожайности на всем массиве под влиянием всех совместно действующих факторов: внесения удобрений, погодных условий, организации работ и т.д.

Межгрупповая дисперсия характеризует вариацию результативного признака, которая происходит под влиянием фактора положенного в основу группировки. Она характеризует колеблемость урожайности под влиянием одного фактора – внесенных удобрений.

Внутригрупповая дисперсия характеризует случайную вариацию. Эта вариация возникает под влиянием других, неучитываемых факторов и не зависит от признака – фактора, положенного в основу группировки.

Правило сложения дисперсий позволяет выявить зависимость результатов от определяющих факторов с помощью соотношения межгрупповой и общей дисперсии. Это соотношение называется коэффициентом детерминации и показывает, какая доля в общей дисперсии приходится на дисперсию, обусловленную вариацией признака, положенного в основу группировки:

Используется правило сложения дисперсий и для определения степени связи между изучаемыми признаками. Для этого необходимо найти эмпирическое корреляционное отношение, которое показывает, насколько тесно связаны исследуемое явление и группировочный признак:

Эмпирическое корреляционное отношение изменяется от 0 до 1. если связь отсутствует, то ƞ_эмп = 0. В этом случае дисперсия групповых средних равна 0, т.е. все групповые средние равны между собой и межгрупповой вариации нет. Это означает, что группировочный признак не влияет на вариацию исследуемого признака х.

Если связь функциональная, то ƞ_эмп = 1. В этом случае дисперсия групповых средних равна общей дисперсии, т.е. не будет внутригрупповой вариации. Это означает, что группировочный признак полностью определяет вариацию изучаемого признака.

Чем больше значение корреляционного отношения приближается к 1, тем полнее (сильнее) корреляционная связь между признаками.

ƞэмп	Связь
	Отсутствует
0 – 0,2	Очень слабая
0,2 – 0,3	Слабая
0,3 – 0,5	Умеренная
0,5 – 0,7	Заметная
0,7 – 0,9	Тесная
0,9 – 0,99	Весьма тесная
	Функциональная

В нашем случае: (67,8%). Это означает, что на 67,8% урожайность картофеля зависит от количества внесенных удобрений и на 32,2% от прочих других факторов.

. Исходя из таблицы в нашем случае у нас наблюдается тесная связь между количеством внесенных удобрений и урожайностью картофеля.