 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Числовая последовательности и ее предел
|
|
Функция f(x) называется функцией целочисленного аргумента, если множество значений x, для которых она определена, является множеством всех натуральных чисел1, 2, 3,… Примером функции целочисленного аргумента может служить сумма n первых чисел натурального ряда. В данном случае
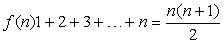
Числовой последовательностью называется бесконечное множество чисел
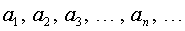 (1)
(1)
следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого 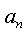 задается как функция целочисленного аргумента,
задается как функция целочисленного аргумента, 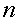 т.е.
т.е. 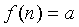 .
.
Число А называется пределом последовательности (1), если для любого 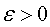 существует число
существует число 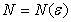 , такое, что при
, такое, что при 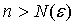 выполняется неравенство
выполняется неравенство 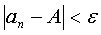 . Если число А есть предел последовательности (1), то пишут
. Если число А есть предел последовательности (1), то пишут
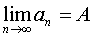
Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся.
Для сходящихся последовательностей имеют место теоремы:
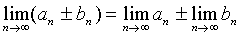
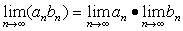
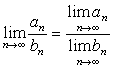
если 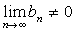 .
.
Предел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении порядкового номера n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение.
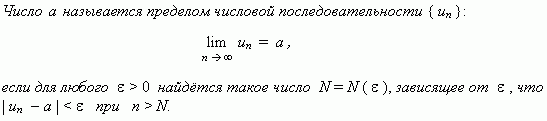
Это определение означает, что a есть предел числовой последовательности, если её общий член неограниченно приближается к a при возрастании n. Геометрически это значит, что для любого > 0 можно найти такое число N, что начиная с n > N все члены последовательности расположены внутри интервала (a -, a +). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.
Последовательность называется ограниченной, если существует такое число M, что | un | 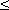 M для всех n. Возрастающая или убывающая последовательность называется монотонной.
M для всех n. Возрастающая или убывающая последовательность называется монотонной.
43.Предел функции. Предел функции в точке. Односторонние пределы. Предел функции при 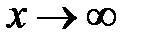 .
.
Дата публикования: 2015-10-09; Прочитано: 411 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
